题目内容
12.(1)计算:已知x=2-$\sqrt{5}$,y=2$\sqrt{5}$,求2x+y的值;(2)已知关于x的一元二次方程x2+2x+m=0
(a)当m=3时,判断方程的根的情况;
(b)当m=-3时,求方程的根.
分析 (1)直接把x和y的值代入2x+y,再化简即可;
(2)(a)m=3代入方程,求出△=b2-4ac即可;
(b)把m=-3代入方程,利用因式分解法求出方程的根.
解答 解:(1)∵x=2-$\sqrt{5}$,y=2$\sqrt{5}$,
∴2x+y=4-2$\sqrt{5}$+2$\sqrt{5}$=4;
(2)(a)当m=3时,
△=b2-4ac=22-4×3=-8,
即原方程无实数根;
(b)当m=-3时,
原方程变为x2+2x-3=0,
即(x-1)(x+3)=0,
x-1=0或x+3=0,
解得x=1或x=-3.
点评 本题主要考查了根的判别式、因式分解法解一元二次方程、分式的化简求值等知识,解答本题的关键是掌握根的判别式与系数的关系,此题难度不大.

练习册系列答案
相关题目
7.菱形和矩形一定具备的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 每条对角线平分一组对角 |
2.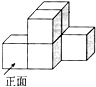 从正面观察下面几何体,能看到的平面图形是( )
从正面观察下面几何体,能看到的平面图形是( )
 从正面观察下面几何体,能看到的平面图形是( )
从正面观察下面几何体,能看到的平面图形是( )| A. | 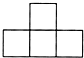 | B. |  | C. |  | D. |  |
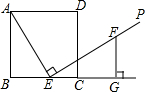 如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.
如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.