题目内容
2．已知a≤5，则化简$\sqrt{（a-5）^{2}}$的结果为5-a．分析 根据$\sqrt{{a}^{2}}$=|a|，可得$\sqrt{（a-5）^{2}}$=|a-5|，再根据绝对值的性质去掉绝对值符号．
解答 解：$\sqrt{（a-5）^{2}}$=|a-5|=5-a，
故答案为：5-a．
点评 此题主要考查了二次根式的性质，关键是掌握$\sqrt{{a}^{2}}$=|a|．
练习册系列答案
相关题目
已知：P为正方形ABCD内一点，△ABP绕点A顺时针旋转后得到的△ADM．
13．下列函数是反比例函数的是（ ）
| A． | y=2x+1 | B． | y=$\frac{3}{x+2}$ | C． | y=$\frac{4}{x^2}$ | D． | y=$\frac{6}{x}$ |
10．若方程6kx-2y=8有一组解$\left\{\begin{array}{l}x=-3\\ y=2\end{array}$，则k的值等于（ ）
| A． | -$\frac{1}{6}$ | B． | $\frac{1}{6}$ | C． | $\frac{2}{3}$ | D． | -$\frac{2}{3}$ |
如图，在直角坐标系中，正方形的中心在原点O，且正方形的一组对边与x轴平行，若正方形的边长是2，则图中阴影部分的面积等于1．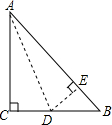
有一块直角三角形纸片，两直角边AC=12cm，BC=5cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD的长为2.4cm．