题目内容
14．
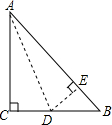有一块直角三角形纸片，两直角边AC=12cm，BC=5cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD的长为2.4cm．
分析 先根据勾股定理求得AB的长，再根据折叠的性质求得AE，BE的长，从而利用勾股定理可求得CD的长．
解答 解：∵AC=12cm，BC=5cm，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13cm，
∵AE=AC=12cm（折叠的性质），
∴BE=1cm，
设CD=x，则在Rt△DEB中，12+x2=（5-x）2，
∴x=2.4cm．
故答案为：2.4cm．
点评 本题考查了折叠的性质以及利用勾股定理解直角三角形，熟练运用折叠的性质和勾股定理是解决问题的关键．
练习册系列答案
相关题目
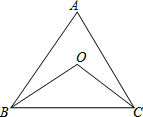如图，点0是△ABC的∠ABC、∠ACB的平分线的交点，
如图，⊙O半径为5，OM⊥弦AB于点M，若OM=3，则弦AB长为8．