题目内容
12.解方程:(1)(2x-1)2=x2+4x+4
(2)2x2+1=3x.
分析 (1)先进行整理,再根据配方法的步骤进行配方,然后开方即可;
(2)先把一次项移到等号的左边,再进行因式分解,然后求解即可.
解答 解:(1)(2x-1)2=x2+4x+4,
4x2-4x+1-x2-4x-4=0,
3x2-8x-3=0,
x2-$\frac{8}{3}$x=1,
x2-$\frac{8}{3}$x+$\frac{16}{9}$=$\frac{25}{9}$,
(x-$\frac{4}{3}$)2=$\frac{25}{9}$,
x-$\frac{4}{3}$=±$\frac{5}{3}$,
x1=3,x2=-$\frac{1}{3}$.
(2)2x2+1=3x,
2x2-3x+1=0,
(2x-1)(x-1)=0,
x1=$\frac{1}{2}$,x2=1.
点评 此题考查了一元二次方程的解法,用到的知识点是配方法的步骤和因式分解,关键是把给出的方程进行变形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17. 如图,在所标识的角中,同位角是( )
如图,在所标识的角中,同位角是( )
 如图,在所标识的角中,同位角是( )
如图,在所标识的角中,同位角是( )| A. | ∠1和∠2 | B. | ∠2和∠3 | C. | ∠1和∠3 | D. | ∠1和∠4 |
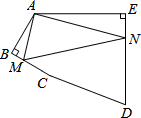 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC,DE上分别找一点M,N,使△AMN的周长最小,则△AMN的最小周长为2$\sqrt{7}$.
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC,DE上分别找一点M,N,使△AMN的周长最小,则△AMN的最小周长为2$\sqrt{7}$. 已知直线y=kx+b(k≠0)过点(-1,6),且与y=-3x-5平行,直线分别交x轴,y轴于A,B 两点.
已知直线y=kx+b(k≠0)过点(-1,6),且与y=-3x-5平行,直线分别交x轴,y轴于A,B 两点.