题目内容
13.下列分式中,属于最简分式的个数是( )①$\frac{4}{2x}$,②$\frac{2x}{{x}^{2}+1}$,③$\frac{x-1}{{x}^{2}-1}$,④$\frac{1-x}{x-1}$,⑤$\frac{{y}^{2}-{x}^{2}}{x+y}$,⑥$\frac{{x}^{2}{+y}^{2}}{{x}^{2}y+x{y}^{2}}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分,即可得出答案.
解答 解:①$\frac{4}{2x}$=$\frac{2}{x}$,不是最简分式;
②$\frac{2x}{{x}^{2}+1}$是最简分式;
③$\frac{x-1}{{x}^{2}-1}$=$\frac{x-1}{(x+1)(x-1)}$=$\frac{1}{x+1}$,不是最简分式;
④$\frac{1-x}{x-1}$=-1,不是最简分式;
⑤$\frac{{y}^{2}-{x}^{2}}{x+y}$=$\frac{(x+y)(y-x)}{x+y}$=y-x,不是最简分式;
⑥$\frac{{x}^{2}{+y}^{2}}{{x}^{2}y+x{y}^{2}}$是最简分式;
属于最简分式有②⑥,共2个;
故选B.
点评 此题考查了最简分式,分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
1.若直角三角形的两条直角边长为a、b,斜边长为c,斜边上的高为h,则下列关系正确的是( )
| A. | a2+b2=2h2 | B. | $\frac{1}{a^2}+\frac{1}{b^2}$=$\frac{1}{h^2}$ | C. | $\frac{1}{a}+\frac{1}{b}$=$\frac{1}{h}$ | D. | ab=h2 |
8.甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均成绩都相同,方差分别是S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,则射箭成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
18.在下列给出的条件中,不能判定四边形ABCD一定是平行四边形的是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AB=CD | D. | AB∥CD,AD∥BC |
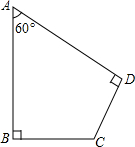 如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.
如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.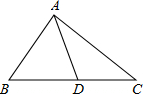 如图,已知△ABC的周长为27cm,AC=9cm,BC边上中线AD=6cm,△ABD周长为19cm,AB=8cm.
如图,已知△ABC的周长为27cm,AC=9cm,BC边上中线AD=6cm,△ABD周长为19cm,AB=8cm.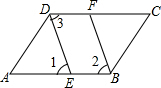 已知:如图,∠ABC=∠ADC,BF、DE是∠ABC、∠ADC的角平分线,DE∥BF.DC和AB有什么位置关系,并加以说明.
已知:如图,∠ABC=∠ADC,BF、DE是∠ABC、∠ADC的角平分线,DE∥BF.DC和AB有什么位置关系,并加以说明.