题目内容
1.若直角三角形的两条直角边长为a、b,斜边长为c,斜边上的高为h,则下列关系正确的是( )| A. | a2+b2=2h2 | B. | $\frac{1}{a^2}+\frac{1}{b^2}$=$\frac{1}{h^2}$ | C. | $\frac{1}{a}+\frac{1}{b}$=$\frac{1}{h}$ | D. | ab=h2 |
分析 由勾股定理推出a、b、h之间的关系即可解答.
解答 解:由a2+b2=c2,ab=ch,
推出c=$\sqrt{{a}^{2}+{b}^{2}}$,
所以$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$=h2,
所以$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$.
故选B.
点评 本题考查了利用勾股定理,灵活运用三边关系得到a、b、h之间的关系是解题的关键.

练习册系列答案
相关题目
12.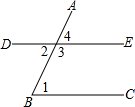 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
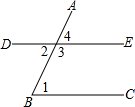 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | ∠1和∠2是同位角 | B. | ∠1和∠4是内错角 | ||
| C. | ∠1和∠3是内错角 | D. | ∠1和∠3是同旁内角 |
16.下列说法中正确的是( )
| A. | 若式子$\sqrt{x-1}$有意义,则x>1 | |
| B. | 已知a,b,c,d都是正实数,且$\frac{a}{b}$<$\frac{c}{d}$,则$\frac{b}{a+b}$<$\frac{d}{c+d}$ | |
| C. | 解分式方程$\frac{x}{x-3}$=2+$\frac{3}{x-3}$的结果是原方程无解. | |
| D. | 在反比例函数y=$\frac{k-2}{x}$中,若x>0时,y随x的增大而增大,则k的取值范围是k>2 |
6.关于x的方程mx-m=-x-1有解,则m的值是( )
| A. | m≠0 | B. | m≠1 | C. | m≠-1 | D. | m≠±1 |
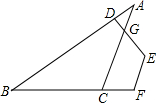 如图,DE⊥AB,EF∥AC,∠A=32°,
如图,DE⊥AB,EF∥AC,∠A=32°,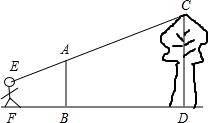 如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD. 如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.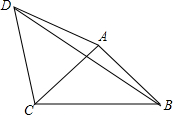 如图,四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45°,则BD的长为$\sqrt{34}$.
如图,四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45°,则BD的长为$\sqrt{34}$.