题目内容
3.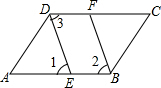 已知:如图,∠ABC=∠ADC,BF、DE是∠ABC、∠ADC的角平分线,DE∥BF.DC和AB有什么位置关系,并加以说明.
已知:如图,∠ABC=∠ADC,BF、DE是∠ABC、∠ADC的角平分线,DE∥BF.DC和AB有什么位置关系,并加以说明.
分析 根据角平分线定义和已知求出∠3=∠2,根据平行线性质求出∠1=∠2,求出∠1=∠3,根据平行线的判定推出即可.
解答 解:DC∥AB,
理由是:∵BF、DE是∠ABC、∠ADC的角平分线,
∴∠3=$\frac{1}{2}$∠ADC,∠2=$\frac{1}{2}$∠ABC,
∵∠ABC=∠ADC,
∴∠3=∠2,
∵DE∥BF,
∴∠1=∠2,
∴∠1=∠3,
∴DC∥AB.
点评 本题考查了角平分线定义,平行线的性质和判定的应用,解此题的关键是推出∠1=∠3,注意:内错角相等,两直线平行.

练习册系列答案
相关题目
15.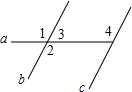 如图,在所标记的角中,同位角是( )
如图,在所标记的角中,同位角是( )
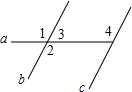 如图,在所标记的角中,同位角是( )
如图,在所标记的角中,同位角是( )| A. | ∠1和∠2 | B. | ∠1和∠4 | C. | ∠1和∠3 | D. | ∠2和∠3 |
12.在Rt△ABC中,∠ACB=90°,AC=CB,CD是斜边AB的中线,若AB=2$\sqrt{2}$,则点D到BC的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{\sqrt{2}}{2}$ |
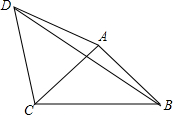 如图,四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45°,则BD的长为$\sqrt{34}$.
如图,四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45°,则BD的长为$\sqrt{34}$.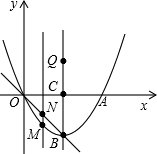 如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).
如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).