题目内容
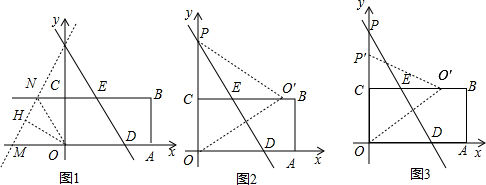
如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=-
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
(Ⅰ)若直线y=-
x+b过矩形OABC对角线交点,求b的值;
(Ⅱ)在(Ⅰ)的条件下,当直线y=-
x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
(Ⅲ)当直线y=-
x+b沿y轴向 平移 个单位长度时,将矩形OABC沿平移后的直线折叠,带你O恰好落在边BC上.

| 3 |
| 2 |
(Ⅰ)若直线y=-
| 3 |
| 2 |
(Ⅱ)在(Ⅰ)的条件下,当直线y=-
| 3 |
| 2 |
(Ⅲ)当直线y=-
| 3 |
| 2 |

考点:一次函数综合题
专题:综合题
分析:(Ⅰ)根据直线y=-
x+b必过矩形的中心,然后求得矩形的中心坐标为(6,3),代入解析式即可求得b值;
(Ⅱ)假设存在ON平分∠CNM的情况,过O作OH⊥PM于H,解得OH=OC=6在直角三角形OPM中OP=12,从而求得∠OPM=30°,利用三角函数求得OM的长,从而求得DM的长;
(Ⅲ)假设沿DE将矩形OABC折叠,点O落在边BC上O′处,连接PO′、OO′,得到△OPO′为等边三角形,从而得到∠OPD=30°,若设沿直线y=-
x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,在Rt△OPD和Rt△OCO′中,利用正切的定义求得a值即可得到将矩形OABC沿直线折叠,点O恰好落在边BC上.
| 3 |
| 2 |
(Ⅱ)假设存在ON平分∠CNM的情况,过O作OH⊥PM于H,解得OH=OC=6在直角三角形OPM中OP=12,从而求得∠OPM=30°,利用三角函数求得OM的长,从而求得DM的长;
(Ⅲ)假设沿DE将矩形OABC折叠,点O落在边BC上O′处,连接PO′、OO′,得到△OPO′为等边三角形,从而得到∠OPD=30°,若设沿直线y=-
| 3 |
| 2 |
解答:解:(Ⅰ)∵直线y=
x+b必过矩形的中心,
由题意得矩形的中心坐标为(6,3),
∴3=
×6+b
解得b=12.
(Ⅱ)假设存在ON平分∠CNM的情况,
过O作OH⊥PM于H,
∵ON平分∠CNM,OC⊥BC,
∴OH=OC=6
由(Ⅰ)知OP=12,
∴∠OPM=30°
∴OM=OP•tan30°=4
当y=0时,由
x+12=0解得x=8,
∴OD=8
∴DM=8-4
.
(Ⅲ) 设沿直线y=
x+a将矩形OABC折叠,点O恰好落在边BC上O′处
连结PO′、OO′,则有P′O′=OP′=a
由题意得:CP′=a-6,∠OPD=∠CO′O
在Rt△OPD中,tan∠OPD=
在Rt△OCO′中,tan∠CO′O=
,
∴
=
,
=
,
解得O′C=9
在Rt△CP′O′中,由勾股定理得:(a-6)2+92=a2
解得a=
,12-
=
,
所以将直线y=-
x+12沿y轴向下平移
个单位得直线y=-
x+
,将矩形OABC沿直线y=-
x+
折叠,点O恰好落在边BC上.
| 3 |
| 2 |
由题意得矩形的中心坐标为(6,3),
∴3=
| 3 |
| 2 |
解得b=12.
(Ⅱ)假设存在ON平分∠CNM的情况,
过O作OH⊥PM于H,
∵ON平分∠CNM,OC⊥BC,
∴OH=OC=6
由(Ⅰ)知OP=12,
∴∠OPM=30°
∴OM=OP•tan30°=4
| 3 |
当y=0时,由
| 3 |
| 2 |
∴OD=8
∴DM=8-4
| 3 |
(Ⅲ) 设沿直线y=
| 3 |
| 2 |
连结PO′、OO′,则有P′O′=OP′=a
由题意得:CP′=a-6,∠OPD=∠CO′O
在Rt△OPD中,tan∠OPD=
| OD |
| OP |
在Rt△OCO′中,tan∠CO′O=
| OC |
| O′C |
∴
| OD |
| OP |
| OC |
| O′C |
| 8 |
| 12 |
| 6 |
| O′C |
解得O′C=9
在Rt△CP′O′中,由勾股定理得:(a-6)2+92=a2
解得a=
| 39 |
| 4 |
| 39 |
| 4 |
| 9 |
| 4 |
所以将直线y=-
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 39 |
| 4 |
| 3 |
| 2 |
| 39 |
| 4 |

点评:本题考查了一次函数的综合运用,注意分类讨论思想的渗透,题目综合性强,难度较大.

练习册系列答案
相关题目
 某衬衫厂,生产某品牌衬衫的成本价位50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍,批发价不低于55元.
某衬衫厂,生产某品牌衬衫的成本价位50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍,批发价不低于55元. 如图,在5×5的正方形网格中,每个小正方形的边长都为1,线段AB的端点都落在格点(即小正方形的顶点)上.请以AB为一边画一个等腰三角形ABC,使点C在格点上,并求所画三角形ABC的面积.
如图,在5×5的正方形网格中,每个小正方形的边长都为1,线段AB的端点都落在格点(即小正方形的顶点)上.请以AB为一边画一个等腰三角形ABC,使点C在格点上,并求所画三角形ABC的面积.
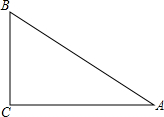 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°. 如图,直线y=kx+b经过A(3,1),B(-1,-3)两点,则不等式
如图,直线y=kx+b经过A(3,1),B(-1,-3)两点,则不等式 如图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=136°,则∠ANM=
如图,在△ABC中,M、N分别是AB、AC的中点,且∠A+∠B=136°,则∠ANM=