题目内容
如图，在△ABC中，M、N分别是AB、AC的中点，且∠A+∠B=136°，则∠ANM=考点：三角形中位线定理
专题：
分析：由三角形内角和定理易得∠C度数，MN是△ABC的中位线，那么所求角的度数等于∠C度数．
解答：解：在△ABC中，∵∠A+∠B=136°，
∴∠ACB=180°-（∠A+∠B）=180°-136°=44°，
∵△ABC中，M、N分别是AB、AC的中点，
∴MN∥BC，
∠ANM=∠ACB=44°．
故答案为：44．
∴∠ACB=180°-（∠A+∠B）=180°-136°=44°，
∵△ABC中，M、N分别是AB、AC的中点，
∴MN∥BC，
∠ANM=∠ACB=44°．
故答案为：44．
点评：本题考查了三角形中位线的性质及三角形内角和定理，中位线定理为证明两条直线平行提供了依据，进而为证明角的相等奠定了基础．
练习册系列答案
优等生题库系列答案
相关题目
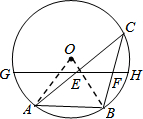如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为9，则GE+FH的最大值为．已知不等式组
（其中a＞b）共有2个整数解，设
=m，则m的取值范围是（ ）
|
| a2-b2 |
| ab |
| A、1＜m＜3 |
| B、-3＜m＜-1或1＜m＜3 |
| C、1≤m＜3 |
| D、-3＜m≤-1或1≤m＜3 |