题目内容
12.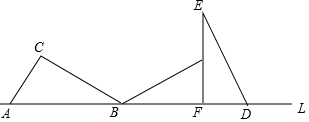 如图,把Rt△ABC的斜边AB放在直线L上,按顺时针方向在L上转动两次使它转到△DEF的位置,设BC=$\sqrt{3}$,AC=1,则点A运动到点D的位置时,点A经过的路线长是多少?点A经过的路线与直线L所围成的面积是多少?
如图,把Rt△ABC的斜边AB放在直线L上,按顺时针方向在L上转动两次使它转到△DEF的位置,设BC=$\sqrt{3}$,AC=1,则点A运动到点D的位置时,点A经过的路线长是多少?点A经过的路线与直线L所围成的面积是多少?
分析 先根据特殊角的三角函数值得出∠ABC的度数,进而可得出∠CBF的度数,由勾股定理求出AB的长,根据弧长公式及扇形的面积公式即可得出结论.
解答 解:∵BC=$\sqrt{3}$,AC=1,
∴tan∠ABC=$\frac{AC}{BC}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,AB=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴∠ABC=30°,
∴∠CBF=150°,
∴点A经过的路线长=$\frac{150π×2}{180}$+$\frac{90π×1}{180}$=$\frac{13π}{6}$.
∴点A经过的路线与直线L所围成的面积=$\frac{150π×4}{360}$+$\frac{90π×1}{360}$=$\frac{23π}{12}$.
点评 本题考查的是轨迹,熟记弧长公式和扇形的面积公式是解答此题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
2.最近以来,我市持续大面积的雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,我校在全校学生中抽取400名同学做了一次调查,调查结果共分为四个等组A.非常了解; B.比较了解:C.基本了解; D.不了解
根据调查统计结果,绘制了不完整的三种统计图表.

对雾霾了解程度的统计表
请结合统计图表,回答下列问题:
(1)本次参与调查的学生选择“A.非常了解”的人数为20人,m=15%,n=35%;
(2)请在图1中补全条形统计图;
(3)请问在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
根据调查统计结果,绘制了不完整的三种统计图表.

对雾霾了解程度的统计表
| 对雾霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| B.比较了解 | m |
| C.基本了解 | 45% |
| D.不了解 | n |
(1)本次参与调查的学生选择“A.非常了解”的人数为20人,m=15%,n=35%;
(2)请在图1中补全条形统计图;
(3)请问在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
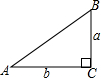 已知Rt△ABC中,两直角边长分别为a=2,b=3,斜边长为c.
已知Rt△ABC中,两直角边长分别为a=2,b=3,斜边长为c.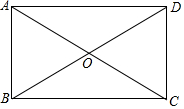 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,BD=6,求矩形ABCD的面积.
如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,BD=6,求矩形ABCD的面积.