题目内容
18.平行四边形ABCD中,cot∠ABC=$\frac{2}{3}$.AB=4,BC=6,则平行四边形的面积为$\frac{72\sqrt{13}}{13}$.分析 过A点向BC边作垂线交BC于E点,然后根据三角函数和勾股定理算出高AE,即可求得答案.
解答 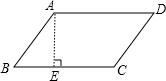 解:过A点向BC边作垂线交BC于E点,如图所示:
解:过A点向BC边作垂线交BC于E点,如图所示:
∵cot∠ABC=$\frac{2}{3}$=$\frac{BE}{AE}$,
设BE=2x,则AE=3x,
在Rt△ABE中,由勾股定理得:(2x)2+(3x)2=42,
解得:x=$\frac{4\sqrt{13}}{13}$,
∴AE=$\frac{12\sqrt{13}}{13}$,
∴平行四边形的面积=BC•AE=6×$\frac{12\sqrt{13}}{13}$=$\frac{72\sqrt{13}}{13}$;
故答案为:$\frac{72\sqrt{13}}{13}$.
点评 本题考查了平行四边形的性质、勾股定理、三角函数;熟练掌握平行四边形的性质,由勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
 如图,点O为正方形ABCD的一边BC的中点,那么正方形ABCD绕点O至少旋转360°度与它本身重合.
如图,点O为正方形ABCD的一边BC的中点,那么正方形ABCD绕点O至少旋转360°度与它本身重合. 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.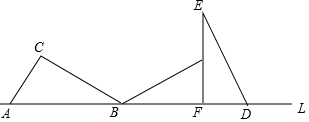 如图,把Rt△ABC的斜边AB放在直线L上,按顺时针方向在L上转动两次使它转到△DEF的位置,设BC=$\sqrt{3}$,AC=1,则点A运动到点D的位置时,点A经过的路线长是多少?点A经过的路线与直线L所围成的面积是多少?
如图,把Rt△ABC的斜边AB放在直线L上,按顺时针方向在L上转动两次使它转到△DEF的位置,设BC=$\sqrt{3}$,AC=1,则点A运动到点D的位置时,点A经过的路线长是多少?点A经过的路线与直线L所围成的面积是多少?