题目内容
3.我们知道:$\frac{1}{1}$-$\frac{1}{2}$=$\frac{1}{1×2}$,$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{2×3}$,┅┅那么反过来也成立如:$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$┅┅,$\begin{array}{l}\frac{1}{n×(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$
利用上面的规律计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+┅┅+$\frac{1}{98×99}$+$\frac{1}{99×100}$
拓展:$\frac{2}{1×3}$+$\frac{2}{3×5}$+$\frac{2}{5×7}$+$\frac{2}{7×9}$+┅┅+$\frac{2}{97×99}$+$\frac{2}{99×101}$.
分析 根据连续整数乘积的倒数等于各自倒数的差可得,根据以上规律列项求解可得.
解答 解:根据题意知$\begin{array}{l}\frac{1}{n×(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+┅┅+$\frac{1}{98×99}$+$\frac{1}{99×100}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{98}$-$\frac{1}{99}$+$\frac{1}{99}$-$\frac{1}{100}$
=1-$\frac{1}{100}$
=$\frac{99}{100}$,
$\frac{2}{1×3}$+$\frac{2}{3×5}$+$\frac{2}{5×7}$+$\frac{2}{7×9}$+┅┅+$\frac{2}{97×99}$+$\frac{2}{99×101}$
=1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{97}$-$\frac{1}{99}$+$\frac{1}{99}$-$\frac{1}{101}$
=1-$\frac{1}{101}$
=$\frac{100}{101}$,
故答案为:$\frac{1}{n}$-$\frac{1}{n+1}$.
点评 本题主要考查数字的变化规律,根据题意得出连续整数乘积的倒数等于各自倒数的差是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.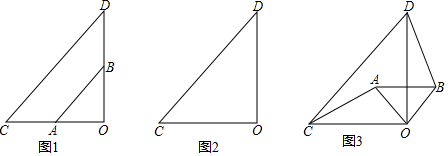
 如图,AD、A′D′分别是△ABC、△A′B′C′的角平分线,且$\frac{AB}{A′B′}$=$\frac{BD}{B′D′}$=$\frac{AD}{A′D′}$.图中有哪几对相似三角形?把它们表示出来,并证明.
如图,AD、A′D′分别是△ABC、△A′B′C′的角平分线,且$\frac{AB}{A′B′}$=$\frac{BD}{B′D′}$=$\frac{AD}{A′D′}$.图中有哪几对相似三角形?把它们表示出来,并证明. 如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,证明:
如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,证明: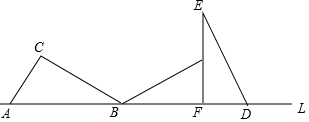 如图,把Rt△ABC的斜边AB放在直线L上,按顺时针方向在L上转动两次使它转到△DEF的位置,设BC=$\sqrt{3}$,AC=1,则点A运动到点D的位置时,点A经过的路线长是多少?点A经过的路线与直线L所围成的面积是多少?
如图,把Rt△ABC的斜边AB放在直线L上,按顺时针方向在L上转动两次使它转到△DEF的位置,设BC=$\sqrt{3}$,AC=1,则点A运动到点D的位置时,点A经过的路线长是多少?点A经过的路线与直线L所围成的面积是多少? 如图,在Rt△ABC中,∠C=90°,AC=2$\sqrt{21}$,sin∠A=$\frac{2}{5}$,求BC的长和tan∠B的值.
如图,在Rt△ABC中,∠C=90°,AC=2$\sqrt{21}$,sin∠A=$\frac{2}{5}$,求BC的长和tan∠B的值.