题目内容
9.如图1是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是多少( )
| A. | 160° | B. | 150° | C. | 120° | D. | 110° |
分析 由矩形的性质可知AD∥BC,由此可得出∠BFE=∠DEF=10°,再根据翻折的性质可知每翻折一次减少一个∠BFE的度数,由此即可算出∠CFE度数.
解答 解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=10°.
由翻折的性质可知:
∠EFC=180°-∠BFE=170°,∠BFC=∠EFC-∠BFE=160°,∠CFE=∠BFC-∠BFE=150°.
故选B.
点评 本题考查了翻折变换以及矩形的性质,解题的关键是找出∠CFE=180°-3∠BFE.本题属于基础题,难度不大,解决该题型题目时,根据翻折变换找出相等的边角关系是关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
20. 有理数a,b在数轴上的位置如图所示,则下列判断正确的是( )
有理数a,b在数轴上的位置如图所示,则下列判断正确的是( )
 有理数a,b在数轴上的位置如图所示,则下列判断正确的是( )
有理数a,b在数轴上的位置如图所示,则下列判断正确的是( )| A. | $\frac{a}{b}$>0 | B. | a+b>0 | C. | |a|<|b| | D. | a-b<0 |
17.已知关于x的一元二次方程中,有两个相等的实数根的方程是( )
| A. | x2+4=0 | B. | 4x2-4x+1=0 | C. | x2+x+3=0 | D. | x2+2x-7=0 |
1. 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )
 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )| A. | 2,$\frac{π}{3}$ | B. | 2$\sqrt{3}$,π | C. | $\sqrt{3}$,$\frac{2π}{3}$ | D. | 2$\sqrt{3}$,$\frac{4π}{3}$ |
 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.若苗圃园的面积为72平方米,求x的值.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.若苗圃园的面积为72平方米,求x的值.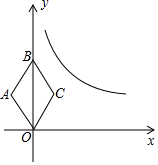 如图,在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$(x>0)的图象和菱形OABC,且OB=4,tan∠BOC=$\frac{1}{2}$.
如图,在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$(x>0)的图象和菱形OABC,且OB=4,tan∠BOC=$\frac{1}{2}$.