题目内容
14.已知二次函数y=x2-4x+c.(1)若该图象过点(4,5),求c的值并求图象的顶点坐标;
(2)若二次函数y=x2-4x+c的图象与坐标轴有2个交点,求字母c的值.
分析 (1)将点(4,5)代入y=x2-4x+c后即可求出c,然后配方即可求出顶点坐标.
(2)抛物线与坐标轴只有两个交点,有两种情况,一是x轴的一个交点与y轴的交点必定重合,即抛物线必过(0,0),另一种是抛物线与x轴只有一个交点,令△=0即可.
解答 解:(1)把(4,5)代入y=x2-4x+c,
∴5=16-16+c,
∴c=5,
∴y=x2-4x+5=(x-2)2+1
∴顶点坐标(2,1)
(2)当抛物线与x轴只有一个交点时,
∴△=0,
∴16-4c=0,
∴c=4,
当抛物线与x轴、y轴的交点重合时,
此时抛物线必过(0,0),
∴c=0,
综上所述,c=4或0
点评 本题考查二次函数图象的性质,涉及抛物线与x轴交点问题,解方程、分类讨论的思想等知识.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
9.如图1是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是多少( )


| A. | 160° | B. | 150° | C. | 120° | D. | 110° |

 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点,S△ABC=9.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点,S△ABC=9.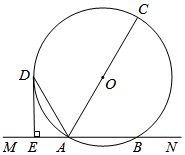 如图,直线MN交⊙O于A,B两点,AC是⊙O的直径,DE与⊙O相切于点D,且DE⊥MN于点E.
如图,直线MN交⊙O于A,B两点,AC是⊙O的直径,DE与⊙O相切于点D,且DE⊥MN于点E.