题目内容
20.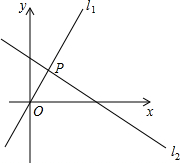 如图,直线l1过原点,直线l2解析式为y=-$\frac{\sqrt{3}}{3}$x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )
如图,直线l1过原点,直线l2解析式为y=-$\frac{\sqrt{3}}{3}$x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )| A. | y=$\frac{1}{3}$x | B. | y=$\frac{\sqrt{3}}{3}$x | C. | y=$\frac{\sqrt{3}}{2}$x | D. | y=$\sqrt{3}$x |
分析 根据直线过原点可设一次函数为y=kx,由两条直线垂直,k之间的关系求出k即可解决问题.
解答 解:∵一次函数经过原点,
∴设所求的一次函数为y=kx,
∵一次函数的图象与直线y=-$\frac{\sqrt{3}}{3}$x+2垂直,
∴k=$\sqrt{3}$,
则直线l1解析式为y=$\sqrt{3}$x,
故选:D.
点评 本题考查一次函数的定义、两条直线垂直k的乘积为-1,解决题目的关键是待定系数法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知一个反比例函数的图象经过点A(3,-4),那么不在这个函数图象上的点是( )
| A. | (-3,-4) | B. | (-3,4) | C. | (2,-6) | D. | ($\frac{\sqrt{2}}{2}$,-12$\sqrt{2}$) |
5.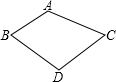 如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )
如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )
 如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )
如图,四边形ABCD,∠A=110°,若点D在AB、AC的垂直平分线上,则∠BDC为( )| A. | 90° | B. | 110° | C. | 120° | D. | 140° |
12.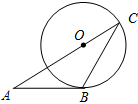 如图,AB与⊙O目切于点B,连接AO,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为( )
如图,AB与⊙O目切于点B,连接AO,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为( )
 如图,AB与⊙O目切于点B,连接AO,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为( )
如图,AB与⊙O目切于点B,连接AO,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为( )| A. | 50° | B. | 25° | C. | 20° | D. | 15° |
11.在函数y=$\frac{{\sqrt{x-3}}}{x-3}$中,自变量x的取值范围是( )
| A. | x>3 | B. | x≥3 | C. | x≠-3 | D. | x>-3且x≠0 |
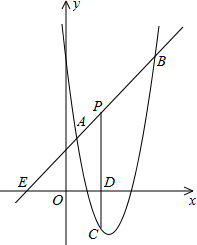 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.