题目内容
7.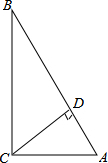 在△ABC中,∠C=90°,解这个直角三角形.
在△ABC中,∠C=90°,解这个直角三角形.(1)∠A=60°,斜边上的高CD=$\sqrt{3}$;
(2)∠A=60°,a+b=3+$\sqrt{3}$.
分析 (1)根据题意可以求得∠B的度数,再根据锐角三角函数可以求得各边的长,从而可以解答本题;
(2)根据题意可以求得∠B的度数,再根据锐角三角函数可以求得a、b的关系,从而可以解答本题.
解答 解:(1)∵在△ABC中,∠C=90°,∠A=60°,
∴∠B=∠C-∠A=90°-60°=30°.
∵斜边上的高CD=$\sqrt{3}$,sinA=$\frac{CD}{AC}$,∠A=60°,
∴AC=2.
∵sinB=$\frac{AC}{AB}$,∠B=30°,tanB=$\frac{AC}{BC}$,
∴AB=4,BC=2$\sqrt{3}$.
即∠B=30°,AC=2,AB=4,BC=2$\sqrt{3}$.
(2))∵在△ABC中,∠C=90°,∠A=60°,
∴∠B=∠C-∠A=90°-60°=30°.
∵tanA=$\frac{a}{b}$,a+b=3+$\sqrt{3}$,∠A=60°,
∴a=3,b=$\sqrt{3}$.
∴c=$\sqrt{{a}^{2}+{b}^{2}}=\sqrt{{3}^{2}+(\sqrt{3})^{2}}=\sqrt{12}=2\sqrt{3}$.
即∠B=30°,AC=$\sqrt{3}$,BC=3,AB=2$\sqrt{3}$.
点评 本题考查解直角三角形,解题的关键是找出所求问题需要的条件,明确锐角三角函数指的是哪两条边的比值.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
17.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{0.3}$ | B. | $\sqrt{\frac{2}{5}xy}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{7a{b}^{3}}$ |
18.小明业余时间进行飞镖训练,上周日训练的平均成绩是8.5环,而这一周训练的平均成绩变化如表:(单位:环)
注:正号表示比前一天提高,负号表示比前一天下降.
本周哪一天的平均成绩最高,它是多少环?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 成绩 | +1 | +0.2 | -0.5 | +0.3 | +0.2 | -0.7 | -0.1 |
本周哪一天的平均成绩最高,它是多少环?
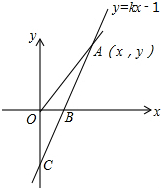 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且OC=2OB.
如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且OC=2OB.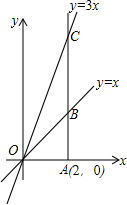 如图所示,已知正比例函数y=x和y=3x,过点A(2,0)作x轴的垂线,与这两个正比例函数的图象分别交与B,C两点,求三角形OBC的面积(其中O为坐标原点).
如图所示,已知正比例函数y=x和y=3x,过点A(2,0)作x轴的垂线,与这两个正比例函数的图象分别交与B,C两点,求三角形OBC的面积(其中O为坐标原点).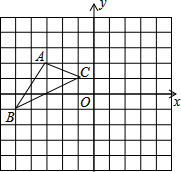 如图,在平面直角坐标系中,△ABC的顶点A的坐标是(-3,2).
如图,在平面直角坐标系中,△ABC的顶点A的坐标是(-3,2).