题目内容
19．当b为-4时，直线y=2x+b与直线y=3x-6的交点在x轴上．分析 先利用x轴上点的坐标特征求出直线y=3x-6与x轴的交点坐标为（2，0），然后把（2，0）代入y=2x+b中即可得到b的值．
解答 解：当y=0时，3x-6=0，解得x=2，则直线y=3x-6与x轴的交点坐标为（2，0），
把（2，0）代入y=2x+b得2×2+b=0，解得b=-4．
故答案为：-4．
点评 本题考查了两直线平行或相交的问题：直线y=k1x+b1（k1≠0）和直线y=k2x+b2（k2≠0）平行，则k1=k2；若直线y=k1x+b1（k1≠0）和直线y=k2x+b2（k2≠0）相交，则交点坐标满足两函数的解析式．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
10．下列说法正确的是（ ）
| A． | 如果∠1=∠2，则∠1和∠2是对顶角 | |
| B． | 锐角的对顶角也是锐角 | |
| C． | 对顶角都是锐角 | |
| D． | 如果∠1和∠2有公共的顶点．则∠1和∠2是对顶角 |
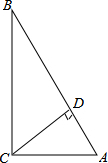在△ABC中，∠C=90°，解这个直角三角形．
已知：如图，在数轴上，点A表示的数为10，点B表示的数为13，点M丧示的数是-20．求：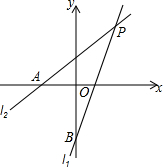
如图，在平面直角坐标系中，直线l1：y=x+1与x轴交于点A，直线l2：y=$\frac{4}{3}$x-1与y轴交于点B，并且直线l1与l2交于点P．
11．下列各式中计算正确的是（ ）
| A． | -1-（-$\frac{1}{2}$）=-1$\frac{1}{2}$ | B． | |a-3|=a-3 | C． | （-7.3）+6.4=-0.9 | D． | 8+|-8|=0 |
8．一次函数y=-x+3与x轴的交点是（ ）
| A． | $（\frac{1}{3}，0）$ | B． | $（-\frac{1}{3}，0）$ | C． | （3，0） | D． | （-3，0） |