题目内容
12．
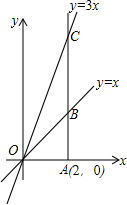如图所示，已知正比例函数y=x和y=3x，过点A（2，0）作x轴的垂线，与这两个正比例函数的图象分别交与B，C两点，求三角形OBC的面积（其中O为坐标原点）．
分析 把点A（2，0）的横坐标分别代入正比例函数y=x和y=3x，求得B、C点的坐标，进一步求得BC的长度，利用三角形的面积求得答案即可．
解答 解：当x=2时，y=x=2，y=3x=6，
点B点的坐标（2，2），C点的坐标（2，6），
则BC=4，
因此三角形OBC的面积=$\frac{1}{2}$×4×2=4．
点评 此题考查两条直线的交点问题，三角形的面积，利用代入的方法求得B、C两点的坐标是解决问题的关键．
练习册系列答案
相关题目
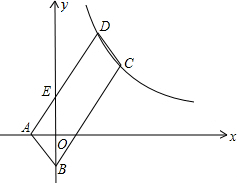如图，?ABCD的顶点A、B的坐标分别是A（-1，0），B（0，-2），顶点C、D在双曲线y=$\frac{k}{x}$上，边AD交y轴于点E，且四边形BCDE的面积是△ABE面积的3倍．
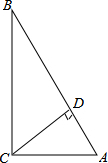在△ABC中，∠C=90°，解这个直角三角形．
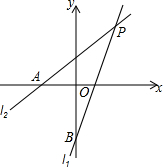如图，在平面直角坐标系中，直线l1：y=x+1与x轴交于点A，直线l2：y=$\frac{4}{3}$x-1与y轴交于点B，并且直线l1与l2交于点P．
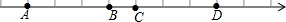已知数轴上A、B、C、D四点对应的数均为整数，且相邻两刻度的距离表示单位长度，若点A对应数a，点B对应数b，
2．给x位学生分配宿舍，x正好是12的倍数．如果每间宿舍住4人，最后多余1间宿舍；如果每间宿舍住3人，最后还缺2间，求学生人数．可列方程（ ）
| A． | $\frac{x-1}{4}$=$\frac{x+2}{3}$ | B． | $\frac{x}{4}$+1=$\frac{x}{3}$-2 | C． | 4（x-1）=3（x+2） | D． | $\frac{x}{4}$-1=$\frac{x}{3}$+2 |