题目内容
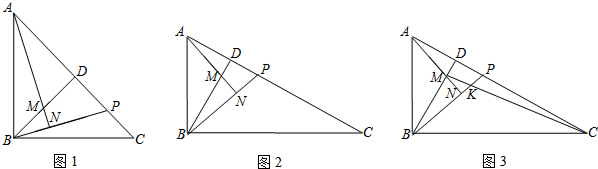
3.已知,在Rt△ABC中,∠ABC=90°,作BD⊥AC,垂足为D,点P为线段DC上一动点(不与点D、C重合),连接BP,作AN⊥BP,垂足为N,设AN交BD于点M.(1)当∠C=45°时(如图1),请证明:CP=BM;
(2)当∠C=30°时(如图2),请直接写出CP与BM的数量关系:CP=$\sqrt{3}$BM;
(3)在(2)问的基础上(如图3),连接MC,设MC交BP于点K,当DP=$\frac{1}{4}$PC=3时,请求MK的长度.
分析 (1)利用等腰直角三角形的性质和全等三角形的判定定理可得△ABM≌△BCP,易得BM=CP;
(2)首先证明△AMB∽△BPC,利用相似三角形的性质易得$\frac{BM}{CP}=\frac{AB}{BC}$,由特殊角的三角函数易得$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$,易得出结论;
(3)连接MP,由DP=$\frac{1}{4}$PC=3,易得CP=12,CD=15,BD=5$\sqrt{3}$,BM=4$\sqrt{3}$,DM=$\sqrt{3}$,CM=2$\sqrt{57}$,证得△DMP∽△DBC,△MKP∽△CKB,利用相似三角形的性质,得$\frac{MK}{CK}$,求得MK的长.
解答 (1)证明:∵∠ABC=90°,∠C=45°,
∴∠BAC=45°,
∴AB=AC,
∵BD⊥AC,
∴∠ABD=45°,∠CBD=∠45°,
∴∠ABD=∠C=∠CBD,
∵AN⊥BP,BD⊥AC,
∴∠MAD=∠MBN,
∴∠MAB=∠PBC,
在△ABM与△BCP中,
$\left\{\begin{array}{l}{∠MAB=∠PBC}\\{AB=CB}\\{∠ABM=∠C}\end{array}\right.$,
∴△ABM≌△BCP(SAS),
∴BM=CP;
(2)解:∵BD⊥AC,∠ABC=90°,
即∠ABD+∠DBC=90°,∠BAD+∠ABD=90°,
∴∠DBC=∠BAD,
由(1)∠DAN=∠DBN,
∴∠MAB=∠PBC,
∵BD⊥AC,AN⊥BP,
∴∠DMN+∠DPN=180°,
∵∠DPN+∠BPC=180°,
∴∠DMN=∠BPC,
∵∠DMN=∠AMB,
∴∠BPC=∠AMB,
∵∠MAB=∠PBC,
∴△AMB∽△BPC,
∴$\frac{BM}{CP}=\frac{AB}{BC}$,
∵∠C=30°,
∴tan∠C=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{BM}{CP}=\frac{\sqrt{3}}{3}$,
∴CP=$\sqrt{3}BM$,
故答案为:CP=$\sqrt{3}$BM;
(3)解:连接MP,由DP=$\frac{1}{4}$PC=3,可得CP=12,CD=15,BD=5$\sqrt{3}$,BM=4$\sqrt{3}$,DM=$\sqrt{3}$,CM=2$\sqrt{57}$,
∵$\frac{DM}{DB}=\frac{DP}{CD}=\frac{1}{5}$,∠BDC=∠MDP,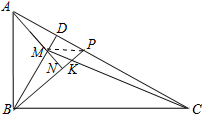
∴△DMP∽△DBC,
∴∠DMP=∠DBC,
∴MP∥BC,
∴△MKP∽△CKB,
∴$\frac{MK}{CK}=\frac{MP}{BC}=\frac{1}{5}$,
∴$\frac{MK}{MC}$=$\frac{1}{6}$,
∴MK=$\frac{1}{6}$MC=$\frac{1}{6}$×$2\sqrt{57}$=$\frac{\sqrt{57}}{3}$.
点评 本题主要考查了全等三角形的判定及性质与相似三角形的判定及性质,锐角三角函数等,利用角的关系找到相似三角形的判定条件是解答此题的关键.

 阅读快车系列答案
阅读快车系列答案(1)设商场购进碳酸饮料y箱,直接写出y与x的函数关系式;
(2)求总利润w关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润.
| 饮料 | 果汁饮料 | 碳酸饮料 |
| 进价(元/箱) | 51 | 36 |
| 售价(元/箱) | 61 | 43 |
| A. | x≥0 | B. | x≥2 | C. | x≤2 | D. | 0≤x≤2 |
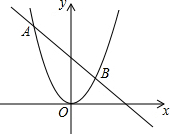 已知函数y1=x2与函数y2=-$\frac{1}{2}$x+3的图象大致如图所示,求抛物线与直线的交点坐标及AB长度.
已知函数y1=x2与函数y2=-$\frac{1}{2}$x+3的图象大致如图所示,求抛物线与直线的交点坐标及AB长度.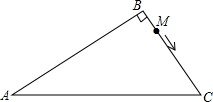 如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,动点M从点B出发以每秒$\sqrt{2}$cm的速度沿B→C→A方向移动到点A,则点M出发几秒后,可使△ABC的面积是△ABM面积的4倍?
如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,动点M从点B出发以每秒$\sqrt{2}$cm的速度沿B→C→A方向移动到点A,则点M出发几秒后,可使△ABC的面积是△ABM面积的4倍?