Question

11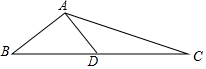．如图，在△ABC中，AB=5，AC=13，边BC上的中线AD=6．
（1）以点D为对称中心，作出△ABD的中心对称图形；
（2）求点A到BC的距离．

Answer 1

分析 （1）延长AD到E使DE=AD，连接CE，则△ABD与△ECD关于点D中心对称；
（2）作AM⊥BC于M，如图，AE=AD+DE12，利用中心对称的性质得CE=AB=5，再利用勾股定理的逆定理可证明△ACE为直角三角形，∠AEC=90°，则∠BAD=90°，然后利用面积法计算出AM即可．

解答 解：（1）如图，△DCE为所作；

（2）作AM⊥BC于M，如图，AE=AD+DE=6+6=12，
∵△ABD与△ECD关于点D中心对称，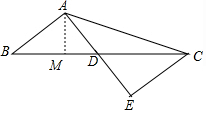
∴CE=AB=5，
在△ACE中，∵CE=5，AE=12，AC=13，
而5²+12²=13²，
∴CE²+AE²=AC²，
∴△ACE为直角三角形，∠AEC=90°，
∴∠BAD=∠AEC=90°，
在Rt△ABD中，BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{5}^{2}+{6}^{2}}$=$\sqrt{61}$，
∵$\frac{1}{2}$AM•BD=$\frac{1}{2}$•AB•AD，
∴AM=$\frac{5×6}{\sqrt{61}}$=$\frac{30\sqrt{61}}{61}$，
即点A到BC的距离为$\frac{30\sqrt{61}}{61}$．

点评 本题考查了作图-旋转变化：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．解决本题的关键是利用勾股定理的逆定理证明∠AEC=90°，从而得到∠BAD=90°．