Question

12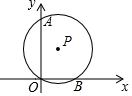．如图，在直角坐标系中，⊙P的圆心坐标为（1，$\sqrt{3}$），半径为2，⊙P分别交y轴，x轴于点A，B，求证：
（1）AB是⊙P的直径；
（2）直线y=$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与⊙P相切于点A．

Answer 1

分析 （1）首先连接OP，AB，过点P作PC⊥OA于点C，由在直角坐标系中，⊙P的圆心坐标为（1，$\sqrt{3}$），可求得OP的长，又由半径为2，可得点O在⊙P上，然后由∠AOB=90°，证得结论；
（2）由直线y=$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$，可求得与x轴，y轴的交点，继而可求得∠OAD与∠OAB的度数，则可求得答案．

解答 证明：（1）连接OP，AB，过点P作PC⊥OA于点C，
∵在直角坐标系中，⊙P的圆心坐标为（1，$\sqrt{3}$），
∴OC=$\sqrt{3}$，PC=1，
∴OP=$\sqrt{P{C}^{2}+O{C}^{2}}$=2，
∵半径为2，
∴点O在⊙P上，
∵∠AOB=90°，
∴AB是⊙P的直径；

（2）设直线y=$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴交于点D，
则点D的坐标为：（-6，0），
∵OA=2OC=2$\sqrt{3}$，
∴tan∠OAD=$\frac{OD}{OA}$=$\sqrt{3}$，
∵AB=2OP=4，
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=2，
∴sin∠OAB=$\frac{OB}{AB}$=$\frac{1}{2}$，
∴∠OAB=30°，
∴∠DAB=90°，
即BA⊥DA，
∴直线y=$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与⊙P相切于点A．

点评 此题考查了切线的判定、垂径定理、圆周角定理以及特殊角的三角函数问题．注意准确作出辅助线是解此题的关键．