题目内容
16.若最简二次根式$\root{m}{m+n-3}$与$\sqrt{8}$是同类二次根式,则$\sqrt{n-2\sqrt{m}}$=$\sqrt{2}$-1.分析 根据同类二次根式的概念列出关系式,求出m、n的值,把m、n的值代入所求的代数式,根据完全平方公式计算即可.
解答 解:$\sqrt{8}$=2$\sqrt{2}$,
由题意得,m=2,m+n-3=2,
解得m=2,n=3,
则$\sqrt{n-2\sqrt{m}}$=$\sqrt{3-2\sqrt{2}}$=$\sqrt{2}$-1,
故答案为:$\sqrt{2}$-1.
点评 本题考查的是同类二次根式的概念,掌握几个二次根式化为最简二次根式后,被开方数相同的二次根式称为同类二次根式是解题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
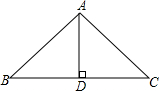 如图,在△ABC中,AB=AC,AD⊥BD于D.若AB=5,BD=4,求△ABC的周长.
如图,在△ABC中,AB=AC,AD⊥BD于D.若AB=5,BD=4,求△ABC的周长.