题目内容
12．观察下列等式：1=12，1+3=22，1+3+5=32，1+3+5+7=42，…，则1+3+5+7+…+2015=1016064．分析 根据1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，可得1+3+5+…+（2n-1）=n2，据此求出1+3+5+…+2015的值是多少即可．
解答 解：因为1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，
所以1+3+5+…+2015
=1+3+5+…+（2×1008-1）
=10082
=1016064
故答案为：1016064．
点评 此题主要考查了探寻数列规律问题，注意观察总结规律，并能正确的应用规律，解答此题的关键是判断出：1+3+5+…+（2n-1）=n2．
练习册系列答案
相关题目
2．
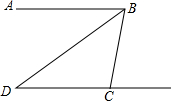如图，AB∥CD，BD平分∠ABC，若∠DCB=100°，则∠D的度数是（ ）
如图，AB∥CD，BD平分∠ABC，若∠DCB=100°，则∠D的度数是（ ）| A． | 40° | B． | 50° | C． | 30° | D． | 45° |
4．
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列，若规定（m、n）表示第m排从左向右第n个数，则（6，5）与（13，6）表示的两数之积是（ ）
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列，若规定（m、n）表示第m排从左向右第n个数，则（6，5）与（13，6）表示的两数之积是（ ）| A． | $\sqrt{6}$ | B． | 6 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |