题目内容
14.等腰三角形一腰上的高与另一腰的夹角为50°,它的底角为20°或70°.分析 根据题意,等腰三角形一腰上的高与另一腰的夹角为50°,分两种情况讨论,①如图1,当一腰上的高在三角形内部时,即∠ABD=50°时,②如图2,当一腰上的高在三角形外部时,即∠ABD=50°时;根据等腰三角形的性质,解答出即可.
解答  解:①如图1,
解:①如图1,
∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠ABD=50°,
∴在直角△ABD中,∠A=90°-50°=40°,
∴∠C=∠ABC=$\frac{180°-40°}{2}$=70°;
②如图2,
∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠ABD=50°,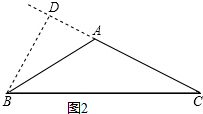
∴在直角△ABD中,∠BAD=90°-50°=40°,
又∵∠BAD=∠ABC+∠C,∠ABC=∠C,
∴∠C=∠ABC=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×40°=20°.
故答案为:70°或20°.
点评 本题主要考查了等腰三角形的性质,知道等腰三角形一腰上的高与另一腰的夹角为50°,有两种情况,一种是高在三角形内部,另一种是高在三角形外部,读懂题意,是解答本题的关键.

练习册系列答案
相关题目
9.下列说法中正确的是( )
| A. | 两个全等三角形成轴对称 | |
| B. | 两个三角形关于某直线对称,不一定全等 | |
| C. | 线段AB的对称轴垂直平分AB | |
| D. | 直线MN垂直平分线段AB,则直线MN是线段AB的对称轴 |
4.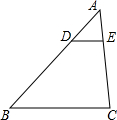 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{EC}=\frac{1}{2}$ | B. | $\frac{DE}{BC}=\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}=\frac{1}{2}$ | D. | $\frac{△ADE的面积}{△ABC的面积}=\frac{1}{3}$ |