题目内容
12. 细图,已知∠MON=90°,在它的两边上截取OA=OB,并在它的内部任作一射线OP,作AD⊥OP于D,BE⊥OP于E.
细图,已知∠MON=90°,在它的两边上截取OA=OB,并在它的内部任作一射线OP,作AD⊥OP于D,BE⊥OP于E.猜想:线段OD与BE,DE与|AD-BE|的大小关系,并说明理由.
分析 先证出∠OAD=∠BOE,由AAS证明△AOD≌△OBE,得出对应边相等OD=BE,AD=OE,即可得出结论.
解答 解:猜想:OD=BE,DE=|AD-BE|;理由如下:
∵∠MONの90°,
∴∠AOD+∠BOE=90°,
∵AD⊥OP,BE⊥OP,
∴∠ADO=∠OEB=90°,
∴∠AOD+∠OAD=90°,
∴∠OAD=∠BOE,
在△AOD和△OBE中,$\left\{\begin{array}{l}{∠ADO=∠OEB}&{\;}\\{∠OAD=∠BOE}&{\;}\\{OA=OB}&{\;}\end{array}\right.$,
∴△AOD≌△OBE(AAS),
∴OD=BE,AD=OE,
∵|AD-BE|=|OE-OD|=|DE|,
∴DE=|AD-BE|.
点评 本题考查了全等三角形的判定与性质、角的互余关系;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
14.当三角形的面积S一定时,它的高h与底边a之间的关系是( )
| A. | 正比例函数关系 | B. | 反比例函数关系 | C. | 一次函数关系 | D. | 不是函数关系 |
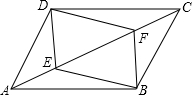 已知:如图,四边形ABCD是平行四边形,DE⊥AC,BF⊥AC,垂足分别是E、F.连结BE、DF.四边形DEBF是什么特殊的四边形?请说明理由.
已知:如图,四边形ABCD是平行四边形,DE⊥AC,BF⊥AC,垂足分别是E、F.连结BE、DF.四边形DEBF是什么特殊的四边形?请说明理由.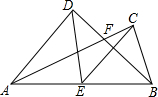 如图.已知AD⊥BD,AC⊥BC,AC与BD交于点F,E为AB的中点,
如图.已知AD⊥BD,AC⊥BC,AC与BD交于点F,E为AB的中点,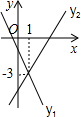 一次函数y1=k1x+b1与y2=k2x+b2的图象如图所示,则当x>1时,y1<y2.
一次函数y1=k1x+b1与y2=k2x+b2的图象如图所示,则当x>1时,y1<y2.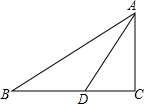 如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AD=$\sqrt{5}$,∠CAD=∠ABC=α,且tanα=$\frac{1}{2}$,则BD的长为( )
如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AD=$\sqrt{5}$,∠CAD=∠ABC=α,且tanα=$\frac{1}{2}$,则BD的长为( ) 如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90°
如图,在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90° 如图,在△ABC中,AD平分∠BAC交BC于D,在AB上截取AE=AC.
如图,在△ABC中,AD平分∠BAC交BC于D,在AB上截取AE=AC.