Question

16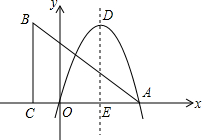．如图，在直角坐标系中，点A，C在x轴上，且AC=8，AB=10，∠ACB=90°
（1）求线段BC的长；
（2）已知抛物线经过坐标原点和点A，若将点B向右平移6个单位后，恰好与抛物线的顶点D重合，求点D的坐标及该抛物线的解析式．

Answer 1

分析 （1）利用勾股定理易求BC的长；
（2）由平移性质得，CE=BD=6，可知AE=OE=2，则D的坐标为（2，6）．设抛物线的解析式为y=a（x-2）²+6，把点A坐标代入求出a的值即可得到抛物线解析．

解答 解：（1）∵BC⊥x轴，即∠BCA=90°，
∴BC=$\sqrt{{AB}^{2}-{AC}^{2}}$=$\sqrt{{10}^{2}-{8}^{2}}$=6．
（2）∵CE=BD=6，
∴AE=OE=2，则D的坐标为（2，6），
设抛物线的解析式为y=a（x-2）²+6，
将点A（4，0）代入得，a（4-2）²+6=0．
∴a=-$\frac{3}{2}$，
∴y=-$\frac{3}{2}$（x-2）²+6．

点评 本题考查了抛物线与x轴的交点、勾股定理、坐标与图形的变化--平移，利用待定系数法求抛物线的解析式以及勾股定理的运用，题目的综合性较强，难度中等