题目内容
2. 如图,求∠A+∠B+∠C+∠D+∠E+∠F 的度数(提示:构造四边形,利用多边形内角和求解)
如图,求∠A+∠B+∠C+∠D+∠E+∠F 的度数(提示:构造四边形,利用多边形内角和求解)
分析 连接AD,由三角形内角和外角的关系可知∠E+∠F=∠ADE+∠DAF,由四边形内角和是360°,即可求∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°.
解答 解:如图,连接AD.
∵∠1=∠E+∠F,∠1=∠ADE+∠DAF,
∴∠E+∠F=∠ADE+∠DAF,
∴∠BAD+∠B+∠C+∠CDA=360°,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°.
故∠A+∠B+∠C+∠D+∠E+∠F的度数是360°.
点评 本题考查的是三角形内角与外角的关系,涉及到四边形及三角形内角和定理,比较简单.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.2014年湖州市许多企业自主创新步伐的加快,专利保护意识的不断增强,我市企业的专利申请量和授权量也不断提高,2014年上半年专利示范企业工业总产值达386.61亿元,用科学记数法表示386.61亿元应该为( )
| A. | 386.61×108 | B. | 0.38661×1011 | C. | 3.8661×1010 | D. | 38.661×109 |
7.已知矩形ABCD中,AB=2BC,在CD上取一点E,使得∠EAB=30°,AE=AB,则∠EBC的度数为( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
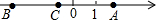 有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简:
有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简: