题目内容
15.已知(a+b)a(a+b)b=(a+b)5,且(a-b)a+4(a-b)4-b=(a-b)7,求aabb的值.分析 根据同底数幂的乘法底数不变指数相加,可得关于a、b的方程组,根据解方程组,可得a、b的值,根据乘方的意义,可得答案.
解答 解:由(a+b)a(a+b)b=(a+b)5,且(a-b)a+4(a-b)4-b=(a-b)7,得
$\left\{\begin{array}{l}{a+b=5}\\{a+4+4-b=7}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$,
aabb=22×(-3)-3=4×$\frac{1}{(-3)^{3}}$=-$\frac{4}{27}$.
点评 本题考查了同底数幂乘法,利用同底数幂的乘法得出方程组解题关键,注意负整数指数幂与正整数指数幂互为倒数.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
17.根据下列表格的对应值:判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<6.17 | B. | 6.17<x<6.18 | C. | 6.18<x<6.19 | D. | 6.19<x<6.20 |
 一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.
一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.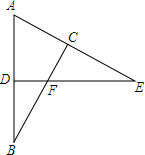 在△ADE中,∠E=22°,延长AD至点B,使得BD=AD,过B点作BC⊥AE,垂足点C,线段BC交边DE于点F,且EF=AB,求∠ADE.
在△ADE中,∠E=22°,延长AD至点B,使得BD=AD,过B点作BC⊥AE,垂足点C,线段BC交边DE于点F,且EF=AB,求∠ADE. 如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?
如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?