题目内容
5.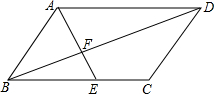 如图,在平行四边形ABCD中,BE:EC=2:1,AE与BD相交于点F,则BF:FD的值为$\frac{2}{3}$.
如图,在平行四边形ABCD中,BE:EC=2:1,AE与BD相交于点F,则BF:FD的值为$\frac{2}{3}$.
分析 由BE:EC=2:1,可求得$\frac{BE}{BC}$,即可求得$\frac{BE}{AD}$,然后根据相似三角形的性质即可得到结论.
解答 解:∵BE:EC=2:1,
∴$\frac{BE}{BC}$=$\frac{2}{3}$,
在平行四边形ABCD中,
∵AD=BC,AD∥BC,
∴△BEF∽△ADF,
∴$\frac{BE}{AD}=\frac{BF}{DF}$,
∴$\frac{BF}{DF}=\frac{BE}{BC}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题主要考查相似三角形的判定和性质,平行四边形的性质,掌握平行四边形的对边平等且相等和相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知反比例函数y=-$\frac{1}{x}$,下列结论正确的是( )
| A. | y的值随着x的增大而减小 | |
| B. | 图象是双曲线,是中心对称图形且是轴对称 | |
| C. | 当x>1时,0<y<1 | |
| D. | 图象可能与坐标轴相交 |
17.根据下列表格的对应值:判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<6.17 | B. | 6.17<x<6.18 | C. | 6.18<x<6.19 | D. | 6.19<x<6.20 |
14.观察如图所示图形,它们是按一定规律排列的,依照此规律,第n个图形中共有( )


| A. | 3n个 | B. | (3n+1)个 | C. | (3n+2)个 | D. | (3n+3)个 |