题目内容
14．在平面直角坐标系中，O为原点，点A的坐标为（1，2），M为y轴上一点，且使得△MOA为等腰三角形，则满足条件的点M的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 分别以O、A为圆心，以OA长为半径作圆，与y轴交点即为所求点M，再作线段OA的垂直平分线，与坐标轴的交点也是所求的点M，作出图形，利用数形结合求解即可．
解答 解：如图，满足条件的点M的个数为4．
故选D．
点评 本题考查了坐标与图形的性质及等腰三角形的判定；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．
练习册系列答案
名校课堂系列答案
相关题目
4．下列几种说法正确的是（ ）
| A． | 0是最小的数 | B． | 最大的负有理数是-1 | ||
| C． | 1是绝对值最小的正数 | D． | 平方等于本身的数只有0和1 |
2．在平面直角坐标系中，A（2，3），O为原点，若点B为坐标轴上一点，且△AOB为等腰三角形，则这样的B点有（ ）
| A． | 6个 | B． | 7个 | C． | 8个 | D． | 9个 |
如图，在线段AB上任取D、C、E三个点，那么这个图中共有几条线段？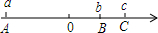
如图，有理数a、b、c在数轴上分别对应点A、B、C点O为原点．