题目内容
7.如图1,把矩形纸片ABCD折叠,使得顶点A与边DC上的动点P重合(P不与点D、C重合),MN为折痕,点M、N分别在边BC、AD上,连结AP、MP、AM,AP与MN相交于点F.(1)试判断AF×AD与AN×AP是否相等?并说明理由;
(2)如图2,过点M、C、P作⊙O,随着点P的运动,若⊙O与AM相切与点M时,⊙O又与AD相切于点H.当AB=2$\sqrt{3}$时,求⊙O的直径MP的长.
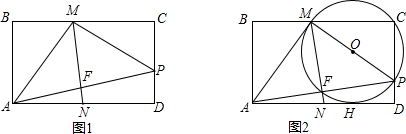
分析 (1)先证明△FAN∽△DAP,由相似三角形的性质可知:$\frac{AF}{AD}=\frac{AN}{AP}$,然后由P不与重合,P在边DC上,可得到AD≠AP,故此判断出AF×AD与AN×AP的关系;
(2)如图1所示:连接OH,并延长HO交MC于点G.先证明△ABM≌△MCP,由全等三角形的性质可求得AB=MC=2$\sqrt{3}$,接下来证明四边形CDHG为矩形,从而可求得GC=HD,然后再依据垂径定理求得HD=$\sqrt{3}$,由切割线定理可求得PD的长,最后在△MCP中依据勾股定理可求得PM的长.
解答 解:(1)AF×AD与AN×AP不相等.
理由:∵点P,点A关于MN对称,
∴MN⊥AP.
∴∠AFN=∠D=90°.
又∵∠FAN=∠DAP,
∴△FAN∽△DAP.
∴$\frac{AF}{AD}=\frac{AN}{AP}$.
∵P不与重合,P在边DC上,
∴AD≠AP,即$\frac{AD}{AP}≠\frac{AP}{AD}$.
∴$\frac{AF}{AN}≠\frac{AP}{AD}$,即AF×AD≠AN×AP.
(2)如图1所示:连接OH,并延长HO交MC于点G.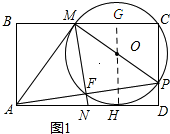
由翻折的性质可知AM=MP.
∵AM为⊙O的切线,
∴OM⊥AM.
∴∠CMP+∠BMA=90°.
又∵∠BAM+∠BMA=90°,
∴∠CMP=∠BAM.
在△ABM和△MCP中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠BAM=∠PMC}\\{AM=MP}\end{array}\right.$,
∴△ABM≌△MCP.
∴AB=MC=2$\sqrt{3}$.
∵DH为⊙O的切线,
∴OH⊥AD.
∴∠GHD=∠D=∠C=90°.
∴四边形CDHG为矩形.
∴HD=GC,OG⊥MC.
∴GC=$\frac{1}{2}$MC=$\sqrt{3}$.
∴HD=$\sqrt{3}$.
由切割线定理可知;HD2=DP•CD,即2$\sqrt{3}$PD=3,解得PD=$\frac{\sqrt{3}}{2}$.
∴CP=2$\sqrt{3}$$-\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
在Rt△MCP中,PM=$\sqrt{M{C}^{2}+C{P}^{2}}$=$\frac{5\sqrt{3}}{2}$.
∴⊙O的直径MP的长为$\frac{5\sqrt{3}}{2}$.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了相似三角形的性质和判定、翻折的性质、切线的性质、全等三角形的性质和判定以及切割线定理、勾股定理、垂径定理等知识点,证得△ABM≌△MCP,然后依据垂径定理和矩形的性质求得HD的长是解题的关键.

 阅读快车系列答案
阅读快车系列答案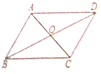 如图,在平行四边形ABCD中,已知AC、BD相交于点O,两条对角线的和为20cm,CD的长为4cm,则△OAB的周长是( )
如图,在平行四边形ABCD中,已知AC、BD相交于点O,两条对角线的和为20cm,CD的长为4cm,则△OAB的周长是( )| A. | 10cm | B. | 8cm | C. | 14cm | D. | 12cm |
| A. | -1 | B. | -3 | C. | 0 | D. | 3 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |