Question

6．（1）请将下表补充完整：

判别式△=b2-4ac	△＞0	△=0	△＜0
二次函数y=ax2+bx+c（a＞0）的图象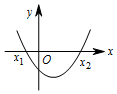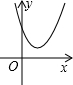
一元二次方程y=ax2+bx+c（a＞0）的根	有两个不相等的实数根 x1=$\frac{-b+\sqrt{△}}{2a}$，x2=$\frac{-b-\sqrt{△}}{2a}$（x1＜x2）	有两个相等的实数根 x1=x2=-$\frac{b}{2a}$	无实数根
使y＞0的x的取值范围	x＜x1或x＞x2	x≠-$\frac{b}{2a}$	全体实数
不等式ax2+bx+c＞0（a＞0）的解集	无解	x≠-$\frac{b}{2a}$	无解

（2）利用你在填上表时获得的收获，解不等式-x²-2x+3＜0（写出过程）；
（3）利用你在填上表时获得的收获，编一个解集为全体实数的一元二次不等式．

Answer 1

分析 解一元二次不等式ax²+bx+c＞0（a≠0）实质上就是求抛物线图象在x轴上方时，自变量的取值范围，抛物线开口方向及与x轴的交点情况就决定了函数值什么情况下大于0，即ax²+bx+c＞0．

解答 解：（1）

判别式 △=b2-4ac	△＞0	△=0	△＜0
二次函数 y=ax2+bx+c（a＞0）的图象
一元二次方程 ax2+bx+c=0（a＞0）的根
使y＞0的x的取值范围		x≠-$\frac{b}{2a}$	全体实数
不等式ax2+bx+c＞0（a＞0）的解集	x＜x1或x＞x2		全体实数
不等式ax2+bx+c＜0（a＞0）的解集	x1＜x＜x2	无解	无解

（2）由原不等式，得x²+2x-3＞0，∵△=4+12＞0，
解方程x²+2x-3=0，得不相等的两个实数根分别为x₁=-3，x₂=1，
∵a=1＞0，∴原不等式的解集为：x＜-3或x＞1；
（若画出函数y=x²+2x-3的图象，并标出与x轴的交点坐标而得解集的，同样可以）
（3）如x²+x+1＞0等，（只要写出满足要求的一个一元二次不等式即可）．

点评 本题主要考查了二次函数的性质与一元二次不等式之间的关系，以及图象与x轴的位置关系．这些性质和规律要求掌握．