题目内容
14.大于-π,而小于2的整数共有( )| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
分析 根据有理数的大小比较法则求出在-π和2之间的整数即可.
解答 解:满足大于-π而小于2的整数有-3,-2,-1,0,1,共有5个.
故选B.
点评 本题考查了有理数的大小比较法则的应用,注意:有理数的大小比较法则是:正数都大于0,负数都小于0,正数大于负数,两个负数比较大小,其绝对值大的反而小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.(1)请将下表补充完整:
(2)利用你在填上表时获得的收获,解不等式-x2-2x+3<0(写出过程);
(3)利用你在填上表时获得的收获,编一个解集为全体实数的一元二次不等式.
| 判别式△=b2-4ac | △>0 | △=0 | △<0 |
| 二次函数y=ax2+bx+c(a>0)的图象 | 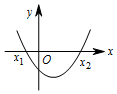 |  | 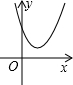 |
| 一元二次方程y=ax2+bx+c(a>0)的根 | 有两个不相等的实数根 x1=$\frac{-b+\sqrt{△}}{2a}$,x2=$\frac{-b-\sqrt{△}}{2a}$(x1<x2) | 有两个相等的实数根 x1=x2=-$\frac{b}{2a}$ | 无实数根 |
| 使y>0的x的取值范围 | x<x1或x>x2 | x≠-$\frac{b}{2a}$ | 全体实数 |
| 不等式ax2+bx+c>0(a>0)的解集 | 无解 | x≠-$\frac{b}{2a}$ | 无解 |
(3)利用你在填上表时获得的收获,编一个解集为全体实数的一元二次不等式.
3.下列命题中:
①等边对等角;
②有两边和一个角分别对应相等的两个三角形全等;
③有一个角是60°的等腰三角形的等边三角形;
④点P(1,-2)在第四象限.
真命题是( )
①等边对等角;
②有两边和一个角分别对应相等的两个三角形全等;
③有一个角是60°的等腰三角形的等边三角形;
④点P(1,-2)在第四象限.
真命题是( )
| A. | ①②④ | B. | ②③ | C. | ①③④ | D. | ③④ |
4.下列因式分解正确的是( )
| A. | x3-4=(x+4)(x-4) | B. | x2+2x+1=x(x+2)+1 | C. | 4x2-2x=2x(2x-1) | D. | 3mx-6my=3m(x-6y) |
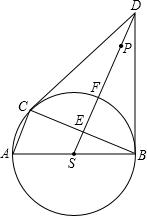 如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点.
如图,在⊙S中,AB是直径,AC、BC是弦,D是⊙S外一点,且DC与⊙S相切于点C,连接CS,DS,DB,其中DS交BC于点E,交⊙S于点F,F为弧BC的中点. 如图所示,已知∠1=115°,∠F=15°,∠B=35°,那么求∠A与∠DEA的度数.
如图所示,已知∠1=115°,∠F=15°,∠B=35°,那么求∠A与∠DEA的度数.