��Ŀ����
2����ͼ����ʾ����֪������y=-x2+4x+5�Ķ���ΪD����x�ύ��A��B���㣨A��B�ң�����y�ύ��C�㣬EΪ��������һ�㣬��C��E���������ߵĶԳ���Գƣ���ֱ��AE����1����ֱ��AE�Ľ���ʽ��
��2����ͼ���У�����ֱ��AE��x�ᷭ�ۺ��������ڵ�F�����F������Ϊ��6��-7����ֱ����գ���
��3����PΪ��������һ���㣬����P��ֱ��PG��y��ƽ�У���ֱ��AE�ڵ�G�����P�ĺ�����Ϊm����S��PGE��S��BGE=2��3ʱ��ֱ��д�����з���������mֵ������˵�����ɣ�
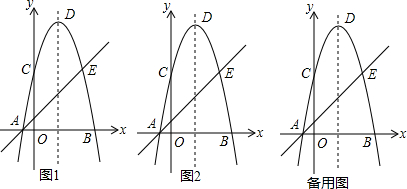
���� ��1�����������ߵĽ���ʽ���ҳ��������ߵĶԳ���Ϊx=2�Լ���A��B��C�����꣬�ɵ�C��������C��E���������ߵĶԳ���Գƣ��������E�����꣬��ֱ��AE�Ľ���ʽΪy=kx+b���ɵ�A��E���������ô���ϵ�����������ֱ��AE�Ľ���ʽ��
��2����ֱ��AF�Ľ���ʽΪy=ax+c���ҳ���E����x��ԳƵĵ�����꣬���øõ��A���������ô���ϵ�����������ֱ��AF�Ľ���ʽ��������ֱ��AF�Լ������ߵĽ���ʽ�ɷ����飬�ⷽ���鼴�������F�����ꣻ
��3������P��PP���ֱ��AE�ڵ�P�䣬����B��BB���ֱ��AE�ڵ�B�䣬���PP��G�͡�BB��AΪ����ֱ�������Σ����ݡ�PGE�͡�BGE������ͬ�ĵױ�GE��S��PGE��S��BGE=2��3�����ɵó�PG��AB=2��3���ɵ�P�ĺ����꼴�ɵó���P��G����������ɵó�PG�ij��ȣ��ٸ���A��B�����꼴�ɵó�AB�ij��ȣ���$\frac{PG}{AB}$=$\frac{2}{3}$���ɵó�|m2-3m-4|=4����֮���ɵó����ۣ�
��� �⣺��1���������ߵĽ���ʽΪy=-x2+4x+5��
��������ߵĶԳ���Ϊ��x=-$\frac{4}{2����-1��}$=2��
��y=-x2+4x+5��x=0����y=5��
���C��������0��5����
��C��E���������ߵĶԳ���Գƣ�
���E��������2��2-0��5��������4��5����
��y=-x2+4x+5��y=0����-x2+4x+5=0��
��ã�x1=-1��x2=5��
���A��������-1��0������B��������5��0����
��ֱ��AE�Ľ���ʽΪy=kx+b��
����A��-1��0����E��4��5������y=kx+b��
�ã�$\left\{\begin{array}{l}{0=-k+b}\\{5=4k+b}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$��
��ֱ��AE�Ľ���ʽΪy=x+1��
��2����ֱ��AF�Ľ���ʽΪy=ax+c��
�ߵ�E������Ϊ��4��5����
���E����x�ĶԳƵ������Ϊ��4��-5����
���㣨-1��0������4��-5������y=ax+c�У�
�ã�$\left\{\begin{array}{l}{0=-a+c}\\{-5=4a+c}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=-1}\\{c=-1}\end{array}\right.$��
��ֱ��AF�Ľ���ʽΪy=-x-1��
����ֱ��AF�������ߵĽ���ʽ�ɷ����飺$\left\{\begin{array}{l}{y=-x-1}\\{y=-{x}^{2}+4x+5}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$����$\left\{\begin{array}{l}{x=6}\\{y=-7}\end{array}\right.$��
���F��������6��-7����
�ʴ�Ϊ��6��-7����
��3������P��PP���ֱ��AE�ڵ�P�䣬����B��BB���ֱ��AE�ڵ�B�䣬��ͼ��ʾ��
��ֱ��AE�Ľ���ʽΪy=x+1��
���PP��G�͡�BB��AΪ����ֱ�������Σ�
�ڡ�PGE�͡�BGE������ͬ�ĵױ�GE����S��PGE��S��BGE=2��3��
��PP�䣺BB��=2��3��
��PG��AB=2��3��
�ߵ�P�ĺ�����Ϊm���ҵ�P��������y=-x2+4x+5��ͼ���ϣ���G��ֱ��y=x+1�ϣ�
���P��������m��-m2+4m+5������G��������m��m+1����
��PG=|-m2+4m+5-��m+1��|=|m2-3m-4|��
�ߵ�B������Ϊ��5��0������A������Ϊ��-1��0����
��AB=5-��-1��=6��
��$\frac{PG}{AB}$=$\frac{|{m}^{2}-3m-4|}{6}$=$\frac{2}{3}$����|m2-3m-4|=4��
��ã�m1=0��m2=3��m3=$\frac{3-\sqrt{41}}{2}$��m4=$\frac{3+\sqrt{41}}{2}$��
�൱S��PGE��S��BGE=2��3ʱ������������mֵΪ0��3��$\frac{3-\sqrt{41}}{2}$��$\frac{3+\sqrt{41}}{2}$��
���� ���⿼���˴���ϵ������������ʽ�����κ��������ʡ���ĶԳơ����Ԫ���η������Լ��㵽ֱ�ߵľ��룬����Ĺؼ��ǣ���1�������E�����ꣻ��2�����ֱ��AF�Ľ���ʽ����3���ҳ�����m�ĺ�����ֵ���ŵ�һԪ���η��̣����������е��⣬�ѶȲ�������������Է����������������Ŀʱ���ҳ�������꣬��ϵ���������ô���ϵ���������������ʽ�ǹؼ���

 һ�������κ������ȱ������ε�λ����ͼ��ʾ������1=50�㣬���2+��3=��������
һ�������κ������ȱ������ε�λ����ͼ��ʾ������1=50�㣬���2+��3=��������| A�� | 190�� | B�� | 130�� | C�� | 100�� | D�� | 80�� |
��1����������У�������1000��������ҵ��ѧ��ÿ��������������ȫ�壻 ��������a=100��
��2������С���Ƶ��b=40��Ƶ��c=0.40��
��3����������110�Σ���110�Σ�����Ϊ��꣬�Թ��Ƹ�У������ҵ��һ���������Ĵ�����Ƕ��٣�
| ��� | �� �� | Ƶ�� | Ƶ�� |
| 1 | 89.5��99.5 | 4 | 0.04 |
| 2 | 99.5��109.5 | 3 | 0.03 |
| 3 | 109.5��119.5 | 45 | 0.45 |
| 4 | 119.5��129.5 | b | c |
| 5 | 129.5��139.5 | 6 | 0.06 |
| 6 | 139.5��149.5 | 2 | 0.02 |
| �� �� | a | 1.00 | |
 ������ABCD�ı߳�Ϊ1���ԶԽ���ACΪ�����ڶ���������ACEF�����ԶԽ���AEΪ����������������AEGH�������ȥ����n�������α߳�Ϊ��������
������ABCD�ı߳�Ϊ1���ԶԽ���ACΪ�����ڶ���������ACEF�����ԶԽ���AEΪ����������������AEGH�������ȥ����n�������α߳�Ϊ��������| A�� | 2n | B�� | 2n-1 | C�� | ��$\sqrt{2}$��n | D�� | ��$\sqrt{2}$��n-1 |
 ��ͼ��ֱ��a��b����ABCΪ����ֱ�������Σ���BAC=90�㣬���1�Ķ����ǣ�������
��ͼ��ֱ��a��b����ABCΪ����ֱ�������Σ���BAC=90�㣬���1�Ķ����ǣ�������| A�� | 22.5�� | B�� | 36�� | C�� | 45�� | D�� | 90�� |
 ��Rt��ABC�У���CAB=90�㣬��P�ǡ�ABC��һ�㣬����ABP�Ƶ�A��ʱ����ת�������ABP���غϣ����AP=6����PP��ij���
��Rt��ABC�У���CAB=90�㣬��P�ǡ�ABC��һ�㣬����ABP�Ƶ�A��ʱ����ת�������ABP���غϣ����AP=6����PP��ij���