题目内容
 如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.
如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.(1)CO是△BCD的高吗?为什么?
(2)求四边形ABCD各内角的度数.
考点:多边形内角与外角,三角形内角和定理
专题:
分析:(1)根据等腰直角三角形的性质,可得∠1=∠2,根据三角形的内角和定理,可得∠DOC的度数,根据三角形高线的定义,可得答案;
(2)根据角的和差、四边形内角和,可得答案.
(2)根据角的和差、四边形内角和,可得答案.
解答:解:(1)CO是△BCD的高,
理由:在△BCD中,∵∠BCD=90°,∠1=∠2,
∴∠1=∠2=90°°÷2=45°.
又∵∠1=∠3,
∴∠3=45°.
∴∴∠DOC=180°-(∠1+∠3)=180°-2×45°=90°,
∴CO⊥DB,
∴CO 是△BCD的高;
(2)∠CDA=∠1+∠4=45°+60°=105°,
∠DCB=90°,
∠DAB=∠5+∠6=30°+30°=60°,
∠ABC=360°-∠CDA-∠DCB-∠DAB
=360°-105°-90°-60°=105°.
理由:在△BCD中,∵∠BCD=90°,∠1=∠2,
∴∠1=∠2=90°°÷2=45°.
又∵∠1=∠3,
∴∠3=45°.
∴∴∠DOC=180°-(∠1+∠3)=180°-2×45°=90°,
∴CO⊥DB,
∴CO 是△BCD的高;
(2)∠CDA=∠1+∠4=45°+60°=105°,
∠DCB=90°,
∠DAB=∠5+∠6=30°+30°=60°,
∠ABC=360°-∠CDA-∠DCB-∠DAB
=360°-105°-90°-60°=105°.
点评:本题考查了多边形内角与外角,利用了等腰直角三角形的性质,三角形的内角和定理,四边形的内角和.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
 填写推理理由:
填写推理理由: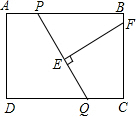 如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为
如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为