题目内容
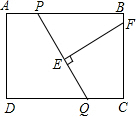 如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为
如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为考点:矩形的性质,线段垂直平分线的性质,勾股定理
专题:
分析:首先连接PF,QF,由线段EF是PQ的垂直平分线,可得PF=QF,又由在矩形ABCD中,AB=8,AD=6,AP=x,BF=y,且AP=CQ,可得方程:(8-x)2+y2=(6-y)2+x2,继而求得答案.
解答: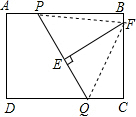 解:连接PF,QF,
解:连接PF,QF,
∵线段EF是PQ的垂直平分线,
∴PF=QF,
∵在矩形ABCD中,AB=8,AD=6,
∴BC=AD=6,
∵AP=x,BF=y,
∴PB=8-x,CF=6-y,
∵CQ=AP=x,
∴在Rt△PBF中,PF2=PB2+BF2=(8-x)2+y2,在Rt△CQF中,QF2=CF2+CQ2=(6-y)2+x2,
∴(8-x)2+y2=(6-y)2+x2,
即y=
x-
.
故答案为:y=
x-
.
 解:连接PF,QF,
解:连接PF,QF,∵线段EF是PQ的垂直平分线,
∴PF=QF,
∵在矩形ABCD中,AB=8,AD=6,
∴BC=AD=6,
∵AP=x,BF=y,
∴PB=8-x,CF=6-y,
∵CQ=AP=x,
∴在Rt△PBF中,PF2=PB2+BF2=(8-x)2+y2,在Rt△CQF中,QF2=CF2+CQ2=(6-y)2+x2,
∴(8-x)2+y2=(6-y)2+x2,
即y=
| 4 |
| 3 |
| 7 |
| 3 |
故答案为:y=
| 4 |
| 3 |
| 7 |
| 3 |
点评:此题考查了矩形的性质、线段垂直平分线的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.
如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6. 已知:如图,∠1=∠2=∠3=50°,则∠4的度数是
已知:如图,∠1=∠2=∠3=50°,则∠4的度数是