题目内容
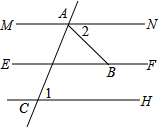 推理填空:如图,MN/EF,GH∥EF,∠CAB=68°,∠1=70°,求∠ABE的度数
推理填空:如图,MN/EF,GH∥EF,∠CAB=68°,∠1=70°,求∠ABE的度数解:
∵MN∥EF,GF∥EF(
∴MN∥
∴∠1+∠CAN=180°(
∵∠1=70°(已知)∴∠CAN=110°
∵∠CAB=68°(已知)∴∠2=42°
∵MN∥EF∴∠ABE=∠2(
∴∠ABE=
考点:平行线的性质
专题:推理填空题
分析:根据平行线的性质可求得∠2,可求得∠ABE=∠2,依次填空即可.
解答:解:∵MN∥EF,GH∥EF ( 已知 )
∴MN∥GH,(平行于同一条直线的两条直线互相平行 )
∴∠1+∠CAN=180°( 两直线平行,同旁内角互补 )
∵∠1=70°(已知)∴∠CAN=110°
∵∠CAB=68°(已知)∴∠2=42°
∵MN∥EF∴∠ABE=∠2(两直线平行,内错角相等 )
∴∠ABE=42°.( 等量代换 )
故答案为:已知;GH;平行一同一条直线的两条件直线互相平行;两直线平行,同旁内角互补;两直线平行,内错角相等;42°;等量代换.
∴MN∥GH,(平行于同一条直线的两条直线互相平行 )
∴∠1+∠CAN=180°( 两直线平行,同旁内角互补 )
∵∠1=70°(已知)∴∠CAN=110°
∵∠CAB=68°(已知)∴∠2=42°
∵MN∥EF∴∠ABE=∠2(两直线平行,内错角相等 )
∴∠ABE=42°.( 等量代换 )
故答案为:已知;GH;平行一同一条直线的两条件直线互相平行;两直线平行,同旁内角互补;两直线平行,内错角相等;42°;等量代换.
点评:本题主要考查平行线的判定和性质,掌握两直线平行,同旁内角互补、内错角相等是解题的关键.

练习册系列答案
相关题目
 如图,时钟的时针、分针、秒针均是匀速转动的,它们分别用OB、OA、OC表示.
如图,时钟的时针、分针、秒针均是匀速转动的,它们分别用OB、OA、OC表示.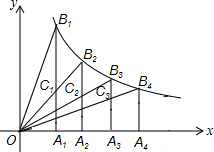 如图,A1,A2,A3,A4是x轴上的点,且OA1=A1A2=A2A3=A3A4,过这些点分别作x轴的垂线交反比例函数y=
如图,A1,A2,A3,A4是x轴上的点,且OA1=A1A2=A2A3=A3A4,过这些点分别作x轴的垂线交反比例函数y=
 三个皮带轮的半径都是1,圆中心距离AC=3,BC=3
三个皮带轮的半径都是1,圆中心距离AC=3,BC=3