题目内容
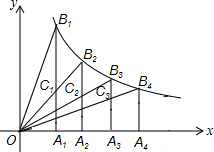 如图,A1,A2,A3,A4是x轴上的点,且OA1=A1A2=A2A3=A3A4,过这些点分别作x轴的垂线交反比例函数y=
如图,A1,A2,A3,A4是x轴上的点,且OA1=A1A2=A2A3=A3A4,过这些点分别作x轴的垂线交反比例函数y=| 4 |
| x |
| S三角形B2C2B4 |
| S梯形C3A3A4B4 |
考点:反比例函数系数k的几何意义
专题:
分析:设OA1=A1A2=A2A3=A3A4=1,则A2(2,0),A3(3,0),A4(4,0),根据反比例函数图象上点的坐标特征得到B2(2,2),B3(3,
),B4(4,1),再利用待定系数法求出OB3的解析式为y=
x,则可确定定C2(2,
),于是根据三角形面积公式可计算出S△B2C2B4=
,同理得到OB4的解析式为y=
x,接着确定C3(3,
),利用梯形的面积公式计算出S四边形C3A3A4B4=
,然后计算
.
| 4 |
| 3 |
| 4 |
| 9 |
| 8 |
| 9 |
| 10 |
| 9 |
| 1 |
| 4 |
| 3 |
| 4 |
| 7 |
| 8 |
| S三角形B2C2B4 |
| S梯形C3A3A4B4 |
解答:解: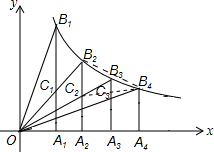 设OA1=A1A2=A2A3=A3A4=1,则A2(2,0),A3(3,0),A4(4,0),
设OA1=A1A2=A2A3=A3A4=1,则A2(2,0),A3(3,0),A4(4,0),
∵点B2,B3,B4都在反比例函数y=
图象上,
∴B2(2,2),B3(3,
),B4(4,1),
设OB3的解析式为y=kx,把B3(3,
)代入得3k=
,解得k=
,
∴OB3的解析式为y=
x,
当x=2时,y=
x=
,则C2(2,
),
∴S△B2C2B4=
×(2-
)×(4-2)=
,
设OB4的解析式为y=mx,把B4(4,1)代入得4m=1,解得m=
,
∴OB4的解析式为y=
x,
当x=3时,y=
x=
,则C3(3,
),
∴S四边形C3A3A4B4=
×(
+1)×(4-3)=
,
∴
=
=
.
故答案为
.
 设OA1=A1A2=A2A3=A3A4=1,则A2(2,0),A3(3,0),A4(4,0),
设OA1=A1A2=A2A3=A3A4=1,则A2(2,0),A3(3,0),A4(4,0),∵点B2,B3,B4都在反比例函数y=
| 4 |
| x |
∴B2(2,2),B3(3,
| 4 |
| 3 |
设OB3的解析式为y=kx,把B3(3,
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
∴OB3的解析式为y=
| 4 |
| 9 |
当x=2时,y=
| 4 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
∴S△B2C2B4=
| 1 |
| 2 |
| 8 |
| 9 |
| 10 |
| 9 |
设OB4的解析式为y=mx,把B4(4,1)代入得4m=1,解得m=
| 1 |
| 4 |
∴OB4的解析式为y=
| 1 |
| 4 |
当x=3时,y=
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∴S四边形C3A3A4B4=
| 1 |
| 2 |
| 3 |
| 4 |
| 7 |
| 8 |
∴
| S三角形B2C2B4 |
| S梯形C3A3A4B4 |
| ||
|
| 80 |
| 63 |
故答案为
| 80 |
| 63 |
点评:本题考查了反比例函数比例系数k的几何意义:在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数图象上点的坐标特征和待定系数法求正比例函数解析式.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,BC⊥AB,连接OC交⊙O于E点,弦AD∥OC,弦DF⊥AB于点G.
如图,AB是⊙O的直径,BC⊥AB,连接OC交⊙O于E点,弦AD∥OC,弦DF⊥AB于点G.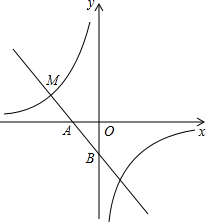 如图,一次函数y=-3x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=
如图,一次函数y=-3x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=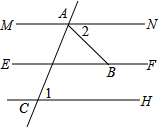 推理填空:如图,MN/EF,GH∥EF,∠CAB=68°,∠1=70°,求∠ABE的度数
推理填空:如图,MN/EF,GH∥EF,∠CAB=68°,∠1=70°,求∠ABE的度数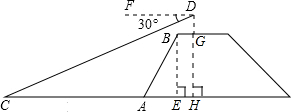 如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号
如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号