题目内容
把下列各式分解因式:
(l)4(a-b)2-16(a+b)2
(2)-x5y3+x3y5.
(l)4(a-b)2-16(a+b)2
(2)-x5y3+x3y5.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)先提取公因式4,再对余下的多项式利用平方差公式继续分解;
(2)先提取公因式-x3y3,再对余下的多项式利用平方差公式继续分解.
(2)先提取公因式-x3y3,再对余下的多项式利用平方差公式继续分解.
解答:解:(1)4(a-b)2-16(a+b)2,
=4[(a-b)2-4(a+b)2],
=4(a-b+2a+2b)(a-b-2a-2b),
=-4(3a+b)(a+3b);
(2)-x5y3+x3y5,
=-x3y3(x2-y2),
=-x2y3(x+y)(x-y).
=4[(a-b)2-4(a+b)2],
=4(a-b+2a+2b)(a-b-2a-2b),
=-4(3a+b)(a+3b);
(2)-x5y3+x3y5,
=-x3y3(x2-y2),
=-x2y3(x+y)(x-y).
点评:本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C2绕点A2;…如此进行下去,得到一条连续的曲线,若P(2013,m)在这条曲线上,则m的值为( )
如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C2绕点A2;…如此进行下去,得到一条连续的曲线,若P(2013,m)在这条曲线上,则m的值为( )| A、4 | B、3 | C、-4 | D、-3 |
下列性质正方形具有而矩形不具有的是( )
| A、四角相等 |
| B、对角线互相垂直 |
| C、对角线相等 |
| D、对角线互相平分 |
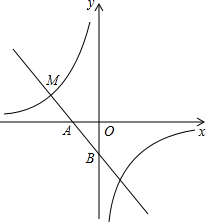 如图,一次函数y=-3x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=
如图,一次函数y=-3x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=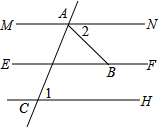 推理填空:如图,MN/EF,GH∥EF,∠CAB=68°,∠1=70°,求∠ABE的度数
推理填空:如图,MN/EF,GH∥EF,∠CAB=68°,∠1=70°,求∠ABE的度数
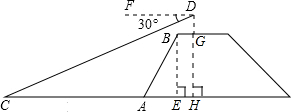 如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号
如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号