题目内容
6.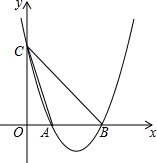 如图所示,直线y=ax2-4ax+b交x轴于A,B两点,交y轴于点C,若A的坐标为(1,0),且△ABC的面积为3,则抛物线的解析式为y=x2-4x+3.
如图所示,直线y=ax2-4ax+b交x轴于A,B两点,交y轴于点C,若A的坐标为(1,0),且△ABC的面积为3,则抛物线的解析式为y=x2-4x+3.
分析 由对称轴计算公式得出x=-$\frac{-4a}{2a}$=2,利用对称性得出点B坐标为(3,0),抛物线与y轴交于点(0,b),利用△ABC的面积为3,求得b,进一步代入点A得出函数解析式即可.
解答 解:∵y=ax2-4ax+b交y轴于点C,对称轴x=-$\frac{-4a}{2a}$=2,A的坐标为(1,0),
∴C(0,b),点B坐标为(3,0),
∵△ABC的面积为3,
∴$\frac{1}{2}$×2×b=3,解得b=3,
把A(1,0)代入y=ax2-4ax+3,解得a=1,
∴抛物线的解析式为y=x2-4x+3.
故答案为:y=x2-4x+3.
点评 此题考查抛物线与x轴的交点问题,待定系数法求函数解析式,求得对称轴,利用抛物线的对称性求得B点坐标的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知点A(3,0)、B(0,4),则线段AB的长度等于( )
| A. | 3 | B. | 4 | C. | 5 | D. | 1 |
14.下列运算正确的是( )
| A. | 2a3÷a2=2a | B. | a2•a3=a6 | C. | (-a2)3=a6 | D. | a+a2=a3 |
15.在对2015个数据进行整理的频数分布直方图中,各组的频数之和与频率之和分别等于( )
| A. | 1,2015 | B. | 2015,2015 | C. | 2015,-2015 | D. | 2015,1 |
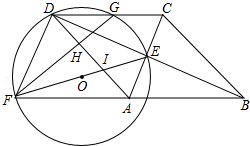 如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.