题目内容
当m<-1时,方程(m3+1)x2+(m2+1)x=m+1的根的情况是( )
| A、两负根 |
| B、两异号根,且正根的绝对值较大 |
| C、两正根 |
| D、两异号根,且负根的绝对值较大 |
考点:一元二次方程根的分布
专题:
分析:首先将方程整理为一般形式,进而利用根据根与系数的关系以及因式分解的应用,分析各式子的符号,进而得出答案.
解答:解:∵(m3+1)x2+(m2+1)x=m+1,
∴(m3+1)x2+(m2+1)x-(m+1)=0,
∴x1x2=
=
=
=
,
∵m<-1,
∴m2-m+1>0,
∴x1x2<0,
∴方程由两异号根,
∵x1+x2=-
=
,
∵m<-1,
∴m2-m+1>0,m+1<0,-(m2+1)<0,
∴x1+x2>0,
∴正根的绝对值较大.
故选:B.
∴(m3+1)x2+(m2+1)x-(m+1)=0,
∴x1x2=
| c |
| a |
| -(m+1) |
| m3+1 |
| -(m+1) |
| (m+1)(m2-m+1) |
| -1 |
| m2-m+1 |
∵m<-1,
∴m2-m+1>0,
∴x1x2<0,
∴方程由两异号根,
∵x1+x2=-
| b |
| a |
| -(m2+1) |
| (m+1)(m2-m+1) |
∵m<-1,
∴m2-m+1>0,m+1<0,-(m2+1)<0,
∴x1+x2>0,
∴正根的绝对值较大.
故选:B.
点评:此题主要考查了一元二次方程根与系数的关系以及因式分解法的应用和有理数运算法则的应用,正确分析得出两根之和以及两根之积的符号是解题关键.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”,若抛物线三角形系数为[-1,b,0]的“抛物线三角形”是等腰直角三角形,则b的值( )
| A、±2 | B、±3 | C、2 | D、3 |
点A是数轴上的任意一点,则下列说法正确的是( )
| A、点A表示的数一定是整数 |
| B、点A表示的数一定是分数 |
| C、点A表示的数一定是有理数 |
| D、点A表示的数可能是无理数 |
下列命题:
①三角形的内心到三角形三个顶点的距离相等;
②如果45°<α<90°,那么sinα>cosα;
③若关于x的方程
=2的解是负数,则m的取值范围为m<-4;
④相等的圆周角所对的弧相等;
⑤对于反比例函数y=
,当x>-1时,y随着x的增大而增大;
其中正确命题有( )
①三角形的内心到三角形三个顶点的距离相等;
②如果45°<α<90°,那么sinα>cosα;
③若关于x的方程
| 3x-m |
| x+2 |
④相等的圆周角所对的弧相等;
⑤对于反比例函数y=
| -2 |
| x |
其中正确命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知二次函数y=-2(x+1)2+4,则( )
| A、其图象的开口向上 |
| B、其图象的对称轴为直线x=1 |
| C、其最大值为4 |
| D、当x<-1时,y随x的增大而减少 |
 已知一次函数y=kx+b的图象如图,则关于x的不等式k(x-4)-2b>0的解集为( )
已知一次函数y=kx+b的图象如图,则关于x的不等式k(x-4)-2b>0的解集为( )| A、x>-2 | B、x<-2 |
| C、x>2 | D、x<3 |
 图中S□ABCD=18cm2,P为BC边上任意一点,M为AP上的一个点,且AM=
图中S□ABCD=18cm2,P为BC边上任意一点,M为AP上的一个点,且AM=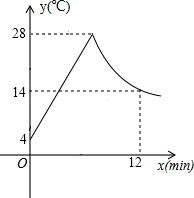 如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.