题目内容
已知抛物线y=ax2+c（a＞0）过A（-3，y1）、B（-7，y2）、C（4，y3）三点，把y1、y2、y3从小到大的顺序排列为 ．
考点：二次函数图象上点的坐标特征
专题：
分析：先求出抛物线的对称轴为y轴和开口方向，再根据二次函数的对称性解答．
解答：解：抛物线y=ax2+c的对称轴为y轴，
∵a＞0，
∴抛物线开口向上，
∵点A、B、C到对称轴的距离分别为3、7、4，
∴y1、y2、y3从小到大的顺序排列为y1＜y3＜y2．
故答案为：y1＜y3＜y2．
∵a＞0，
∴抛物线开口向上，
∵点A、B、C到对称轴的距离分别为3、7、4，
∴y1、y2、y3从小到大的顺序排列为y1＜y3＜y2．
故答案为：y1＜y3＜y2．
点评：本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的对称性和增减性以及开口方向，利用性质求解更加简便．
练习册系列答案
相关题目
如图，已知△ABC，以点B为圆心，AC长为半径画弧；以点C为圆心，AB长为半径画弧，两弧交于点D，且A、D在BC异侧，连接AD．根据题意画出图形，并测量线段AD的长（精确到0.1cm）．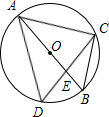
如图，AB是⊙O的直径，△ACD为正三角形，则∠BAC=