题目内容
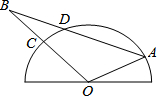如图，半圆O是一个量角器，△AOB为一纸片，AB交半圆于点D，交半圆于点C，若点C、D、A在量角器上对应读数分别为45°，70°，160°，∠B的度数为考点：圆周角定理
专题：
分析：连结OD，如图，根据题意得∠DOC=25°，∠AOD=90°，由于OD=OA，则∠ADO=45°，然后利用三角形外角性质得∠ADO=∠B+∠DOB，所以∠B=45°-25°=20°
解答：
解：连结OD，
如图，则∠DOC=70°-45°=25°，∠AOD=160°-70°=90°，
∵OD=OA，
∴∠ADO=45°，
∵∠ADO=∠B+∠DOB，
∴∠B=45°-25°=20°．
故答案为：25°．
解：连结OD，如图，则∠DOC=70°-45°=25°，∠AOD=160°-70°=90°，
∵OD=OA，
∴∠ADO=45°，
∵∠ADO=∠B+∠DOB，
∴∠B=45°-25°=20°．
故答案为：25°．
点评：本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．
练习册系列答案
相关题目
如图，在△ABC中，∠A=30°，∠B=45°，AC=2
图中S□ABCD=18cm2，P为BC边上任意一点，M为AP上的一个点，且AM=如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”，[a，b，c]称为“抛物线三角形系数”，若抛物线三角形系数为[-1，b，0]的“抛物线三角形”是等腰直角三角形，则b的值（ ）
| A、±2 | B、±3 | C、2 | D、3 |
点A是数轴上的任意一点，则下列说法正确的是（ ）
| A、点A表示的数一定是整数 |
| B、点A表示的数一定是分数 |
| C、点A表示的数一定是有理数 |
| D、点A表示的数可能是无理数 |
已知二次函数y=-2（x+1）2+4，则（ ）
| A、其图象的开口向上 |
| B、其图象的对称轴为直线x=1 |
| C、其最大值为4 |
| D、当x＜-1时，y随x的增大而减少 |