题目内容
已知等腰梯形ABCD中，AD∥BC，AB∥BC，AD＜BC，AD=10，CD=3，如果M为AD上一点，且满足∠BMC=∠A，求AM的长．
考点：等腰梯形的性质
专题：
分析：证明△ABM∽△MDC，根据相似比求得AM的长即可．
解答：
解：如图，在等腰梯形ABCD中，∵AD∥BC，
∴∠A=∠D，
又∵∠A=∠BMC，∠1+∠2=∠3+∠BMC，
∴∠1=∠3，
∴△ABM∽△MDC，
∴
=
∵AB=DC（已知），
设AM=x，则
=
，
∴x2-10x+9=0，
∴x=1或x=9，
∴AM的长为1或9．
解：如图，在等腰梯形ABCD中，∵AD∥BC，∴∠A=∠D，
又∵∠A=∠BMC，∠1+∠2=∠3+∠BMC，
∴∠1=∠3，
∴△ABM∽△MDC，
∴
| AM |
| AB |
| DC |
| DM |
∵AB=DC（已知），
设AM=x，则
| x |
| 3 |
| 3 |
| 10-x |
∴x2-10x+9=0，
∴x=1或x=9，
∴AM的长为1或9．
点评：本题主要考查了等腰梯形的性质，相似三角形的判定及性质，求得三角形相似是本题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
如图，AB是⊙O的直径，MN是弦，AE⊥MN于E，BF⊥MN于F，AB=10，连EO并延长交BF于S．
如图，点C、D在线段AB上，⊙O、⊙O1、⊙O2、⊙O3的直径分别为AB、AC、CD、DB．
如图，E为AD的中点，BE平分∠ABC，且AB+CD=BC，求证：CE平分∠BCD．
已知如图，AB⊥CD，BE是⊙O的直径，若AC=3，求DE．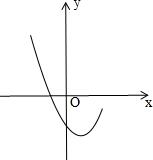
已知二次函数y=x2-2x+c的部分图象如图所示．