题目内容
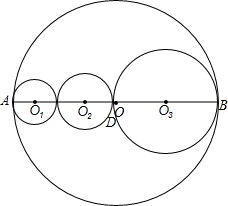 如图,点C、D在线段AB上,⊙O、⊙O1、⊙O2、⊙O3的直径分别为AB、AC、CD、DB.
如图,点C、D在线段AB上,⊙O、⊙O1、⊙O2、⊙O3的直径分别为AB、AC、CD、DB.(1)求⊙O、⊙O1、⊙O2、⊙O3的周长C、C1、C2、C3;
(2)C与C1、C2、C3有怎样的数量关系.
考点:相切两圆的性质
专题:
分析:(1)直接利用圆的周长公式求出即可;
(2)利用(1)中所求得出C与C1、C2、C3的数量关系.
(2)利用(1)中所求得出C与C1、C2、C3的数量关系.
解答: 解:(1)如图所示:∵⊙O、⊙O1、⊙O2、⊙O3的周长C、C1、C2、C3;
解:(1)如图所示:∵⊙O、⊙O1、⊙O2、⊙O3的周长C、C1、C2、C3;
∴C=ABπ,C1=ACπ,C2=CDπ,C3=BDπ;
(2)由(1)得,
ABπ=ACπ+CDπ+BDπ=(AC+CD+BD)π,
故C与C1、C2、C3的数量关系为:C=C1+C2+C3.
 解:(1)如图所示:∵⊙O、⊙O1、⊙O2、⊙O3的周长C、C1、C2、C3;
解:(1)如图所示:∵⊙O、⊙O1、⊙O2、⊙O3的周长C、C1、C2、C3;∴C=ABπ,C1=ACπ,C2=CDπ,C3=BDπ;
(2)由(1)得,
ABπ=ACπ+CDπ+BDπ=(AC+CD+BD)π,
故C与C1、C2、C3的数量关系为:C=C1+C2+C3.
点评:此题主要考查了相切两圆的性质以及圆的周长公式,正确应用圆的周长公式是解题关键.

练习册系列答案
相关题目
根据条件列方程:“x比它的
少4”的数量关系,正确的是( )
| 1 |
| 2 |
A、x-
| ||
B、x+
| ||
C、x-
| ||
D、
|
 若用a表示
若用a表示| 3 | -10 |
| A、A | B、B | C、C | D、D |
 如图,反比例函数y=
如图,反比例函数y= 如图,OE是⊙O的半径,弦AB垂直平分OE,点D是
如图,OE是⊙O的半径,弦AB垂直平分OE,点D是