题目内容
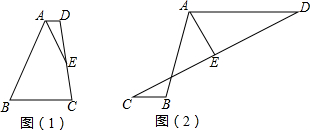
如图(1),线段AD∥BC,连接AB、CD,取CD中点E,连接AE,AE平分∠BAD.
(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.
(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.
(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.
(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.

考点:全等三角形的判定与性质
专题:
分析:(1)延长AE,BF交于点F,即可求证△ADE≌△FCE,即可求得CF=AD,AB=BF,即可求得AB=AD+BC;
(2)不成立,新的结论为:AB+BC=AD.延长AE,BF交于点F,可证△ADE≌△FCE和AB=BF,即可解题.
(2)不成立,新的结论为:AB+BC=AD.延长AE,BF交于点F,可证△ADE≌△FCE和AB=BF,即可解题.
解答:解:(1)延长AE,BF交于点F,

∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴AB=BF,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=AD,
∵BF=BC+CF,
∴AB=BC+AD;
(2)不成立,新结论为:AB=AD-BC.
延长AE,BF交于点F,

证明:∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴AB=BF,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=AD,
∵BF+BC=CF,
∴AB+BC=AD.

∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴AB=BF,
在△ADE和△FCE中,
|
∴△ADE≌△FCE(AAS),
∴CF=AD,
∵BF=BC+CF,
∴AB=BC+AD;
(2)不成立,新结论为:AB=AD-BC.
延长AE,BF交于点F,

证明:∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴AB=BF,
在△ADE和△FCE中,
|
∴△ADE≌△FCE(AAS),
∴CF=AD,
∵BF+BC=CF,
∴AB+BC=AD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADE≌△FCE是解题的关键.

练习册系列答案
相关题目
| 3 |
| 2 |
| • |
| 2 |
| • |
| 6 |
| 9 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 已知动点A在反比例函数y=
已知动点A在反比例函数y=