题目内容
 如图,E为AD的中点,BE平分∠ABC,且AB+CD=BC,求证:CE平分∠BCD.
如图,E为AD的中点,BE平分∠ABC,且AB+CD=BC,求证:CE平分∠BCD.考点:全等三角形的判定与性质
专题:证明题
分析:在BC上找到F点,使得BF=AB,易证△ABE≌△FBE,可得DE=EF,进而可以证明△FCE≌△DCE即可解题.
解答:解:在BC上找到F点,使得BF=AB,
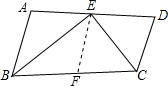
∵AB+CD=BC,BF=AB,
∴CD=CF,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
在△ABE和△FBE中,
,
∴△ABE≌△FBE(SAS)
∴EF=AE,
∵E是AD中点,
∴AE=DE,
∴DE=EF
在△FCE和△DCE中,
,
∴△FCE≌△DCE(SSS),
∴∠FCE=∠DCE,即CE平分∠BCD.

∵AB+CD=BC,BF=AB,
∴CD=CF,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
在△ABE和△FBE中,
|
∴△ABE≌△FBE(SAS)
∴EF=AE,
∵E是AD中点,
∴AE=DE,
∴DE=EF
在△FCE和△DCE中,
|
∴△FCE≌△DCE(SSS),
∴∠FCE=∠DCE,即CE平分∠BCD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABE≌△FBE是解题的关键.

练习册系列答案
相关题目
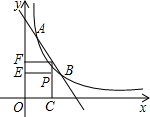 如图,反比例函数y=
如图,反比例函数y=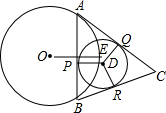 如图,OE是⊙O的半径,弦AB垂直平分OE,点D是
如图,OE是⊙O的半径,弦AB垂直平分OE,点D是
 如图,在△ABC中,∠ACB=90°,AC=BC,FB⊥BC于点B,点D在BC上,AD、CF相交于点E,当AD与CF满足怎样的数量关系时,AE⊥CF,并说明理由.
如图,在△ABC中,∠ACB=90°,AC=BC,FB⊥BC于点B,点D在BC上,AD、CF相交于点E,当AD与CF满足怎样的数量关系时,AE⊥CF,并说明理由. 已知:如图,⊙O中,AB=AC,OD⊥AB于D,OE⊥AC于E.求证:OD=OE.
已知:如图,⊙O中,AB=AC,OD⊥AB于D,OE⊥AC于E.求证:OD=OE.