题目内容
 如图,AB是⊙O的直径,MN是弦,AE⊥MN于E,BF⊥MN于F,AB=10,连EO并延长交BF于S.
如图,AB是⊙O的直径,MN是弦,AE⊥MN于E,BF⊥MN于F,AB=10,连EO并延长交BF于S.(1)证明:AE=BS;
(2)若MN=8,求BF-AE的值.
考点:垂径定理,全等三角形的判定与性质,梯形中位线定理
专题:
分析:(1)由平行可知∠SBO=∠EAO,结合条件可证明△AOE≌△BOS,可得AE=BS;
(2)连接OM,过O作OH⊥MN于点H,则可知OH为△EFS的中位线,且在Rt△OHM中可求得OH=3,则可得FS=2OH=6,结合(1)可得BF-AE=BF-BS=FS=6.
(2)连接OM,过O作OH⊥MN于点H,则可知OH为△EFS的中位线,且在Rt△OHM中可求得OH=3,则可得FS=2OH=6,结合(1)可得BF-AE=BF-BS=FS=6.
解答:(1)证明:∵AE⊥MN,BF⊥MN,
∴AE∥BF,
∴∠OAE=∠OBS,
在△OAE和△OBS中,
,
∴△OAE≌△OBS(AAS),
∴AE=BS;
(2)解:如图,连接OM,过O作OH⊥MN于点H,

则MH=
MN=4,且AB=10,可得OM=5,
在Rt△OMH中,由勾股定理可得OH=3,
又由(1)可知△OAE≌△OBS,
∴OE=OS,
∴O为ES中点,
∴OH为△EFS的中位线,
∴FS=2OH=6,
∴BF-AE=BF-BS=FS=6.
∴AE∥BF,
∴∠OAE=∠OBS,
在△OAE和△OBS中,
|
∴△OAE≌△OBS(AAS),
∴AE=BS;
(2)解:如图,连接OM,过O作OH⊥MN于点H,

则MH=
| 1 |
| 2 |
在Rt△OMH中,由勾股定理可得OH=3,
又由(1)可知△OAE≌△OBS,
∴OE=OS,
∴O为ES中点,
∴OH为△EFS的中位线,
∴FS=2OH=6,
∴BF-AE=BF-BS=FS=6.
点评:本题主要考查垂径定理及全等三角形的判定和性质,掌握过圆心垂直弦的直径平分弦是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| 3 |
| 2 |
| • |
| 2 |
| • |
| 6 |
| 9 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
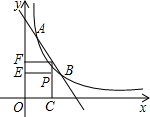 如图,反比例函数y=
如图,反比例函数y=