题目内容
19.为推进阳光体育活动的开展,我校七年级(1)班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与且每人都参加了其中一个活动小组,各活动小组人数分布情况的扇形图和条形图如图所示.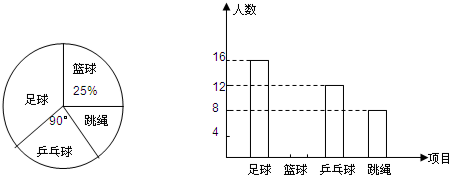
根据以上信息:
(1)求该班共有学生多少名学生?
(2)求跳绳人数所占扇形圆心角是多少度?
(3)补全条形图的空缺部分.
分析 (1)根据喜欢乒乓球的有12人,所占的比例就是扇形统计图中对应的圆心角所对的比例,据此即可求得该班的人数;
(2)利用360°乘以对应的比例即可求得;
(3)利用总人数乘以对应的比例求得喜欢篮球的人数,从而补全直方图.
解答 解:(1)该班的人数是12÷$\frac{90}{360}$=48(人);
(2)跳绳人数所占扇形圆心角是:360°×$\frac{8}{48}$=60°;
(3)喜欢篮球的人数是48×25%=12(人). .
.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
4.若规定sin(α-β)=sinαcosβ-cosαsinβ,则sin15°=( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ |
11. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x+1的图象上,阴影图形
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x+1的图象上,阴影图形 的面积从左向右依次记为S1,S2,S3…Sn,则Sn的值为( )
的面积从左向右依次记为S1,S2,S3…Sn,则Sn的值为( )
 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x+1的图象上,阴影图形
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x+1的图象上,阴影图形 的面积从左向右依次记为S1,S2,S3…Sn,则Sn的值为( )
的面积从左向右依次记为S1,S2,S3…Sn,则Sn的值为( )| A. | Sn=3×22n+1 | B. | Sn=3×22n+3 | C. | Sn=3×22n-3 | D. | Sn=3×22n |
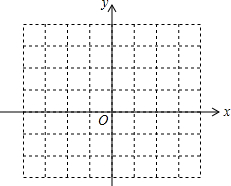 在平面直角坐标系中有一正方形网格,毎个小正方形的边长均为1,四边形各顶 点的坐标分别为A(1,1),B(3,1),C(3,2),D(2,3).
在平面直角坐标系中有一正方形网格,毎个小正方形的边长均为1,四边形各顶 点的坐标分别为A(1,1),B(3,1),C(3,2),D(2,3). 如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.
如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.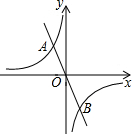 如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A,B,若点A的坐标为(-2,3),则点B的坐标为(2,-3).
如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A,B,若点A的坐标为(-2,3),则点B的坐标为(2,-3).