题目内容
11. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x+1的图象上,阴影图形
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x+1的图象上,阴影图形 的面积从左向右依次记为S1,S2,S3…Sn,则Sn的值为( )
的面积从左向右依次记为S1,S2,S3…Sn,则Sn的值为( )| A. | Sn=3×22n+1 | B. | Sn=3×22n+3 | C. | Sn=3×22n-3 | D. | Sn=3×22n |
分析 根据直线解析式判断出直线与x轴的夹角为45°,从而得到直线与正方形的边围成的三角形是等腰直角三角形,再根据点A的坐标求出正方形的边长并得到变化规律表示出第n个和第n+1个正方形的边长,然后根据阴影部分的面积等于两个等腰直角三角形的面积再减去一个钝角三角形的面积列式求解并根据结果的规律解答即可.
解答 解:∵函数y=x与x轴的夹角为45°,
∴直线y=x+1与正方形的边围成的三角形是等腰直角三角形,
∴A1(0,1),A2(1,2),A3(3,4),
∴第1个正方形的边长为1,
第2个正方形的边长为2,
第3个正方形的边长为4,
第4个正方形的边长为8,
…,
第n个正方形的边长为2n-1,
由图可知,S1=$\frac{1}{2}$×1×1+$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×1=$\frac{3}{2}$,
S2=$\frac{1}{2}$×4×4+$\frac{1}{2}$×2×2-$\frac{1}{2}$×4×2=6,
…,
第n个正方形的边长为2n-1,第n+1个正方形的边长为2n,
Sn=$\frac{1}{2}$•2n-1•2n-1+$\frac{1}{2}$•2n•2n-$\frac{1}{2}$•2•2n-1=3×22n-3.
故选C.
点评 本题考查了正方形的性质,三角形的面积,一次函数图象上点的坐标特征,依次求出各正方形的边长是解题的关键,难点在于求出阴影Sn所在的正方形和正方形的边长.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
2.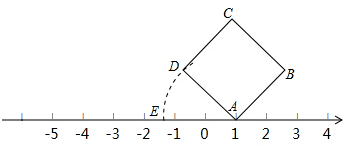 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )| A. | $-\sqrt{5}$ | B. | $1-\sqrt{5}$ | C. | $\frac{{-1-\sqrt{5}}}{2}$ | D. | $\frac{3}{2}-\sqrt{5}$ |
 如图,∠AOC是直角,OC为∠BOD的平分线,且∠AOB=55°,求∠AOD的度数.
如图,∠AOC是直角,OC为∠BOD的平分线,且∠AOB=55°,求∠AOD的度数.
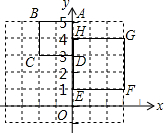 如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是(0,$\frac{17}{5}$),(-6,7).
如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是(0,$\frac{17}{5}$),(-6,7). 按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第二次得到的结果为12,…,则第2016次得到的结果为-1.
按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第二次得到的结果为12,…,则第2016次得到的结果为-1.